Questions on Solving Linear Equations
Questions on solving linear equations may be some of the easiest equation questions that you will see on your exam.
Some of the simplest questions on linear equations will involve only addition or subtraction.
A very basic question may look like the following example:
x + y + 3 = 6
To solve the above equation, you need to isolate x to one side of the equation.
Now look at the solution that follows.
x + y + 3 = 6
First, deal with the integer.
x + y + 3 = 6
x + y + 3 − 3 = 6 − 3
Then perform the operations.
x + y + 3 − 3 = 6 − 3
x + y = 3
Finally, isolate x to find the solution for this basic linear equation.
x + y = 3
x + y − y = 3 − y
x = 3 − y
General Equation of a Straight Line
The following equation can be used for any straight line:
ax + by + c = 0
We can deduce a couple of important points from this equation.
First of all, we can put in 0 for y in order to find the point where the line meets the x axis.
This is called the x intercept.
Equation for the x intercept
ax + by + c = 0
ax + 0y + c = 0
ax + c = 0
ax + c − c = 0 − c
ax = −c
\(x = \frac{-c}{a}\)
Secondly, we can put in 0 for x in order to find the point where the line meets the y axis.
This is called the y intercept.
Equation for the y intercept
ax + by + c = 0
a0 + by + c = 0
by + c = 0
by + c − c = 0 − c
by = −c
\(y = \frac{-c}{b}\)
Plotting Linear Equations
Now look at how we can plot a line on the coordinate plane.
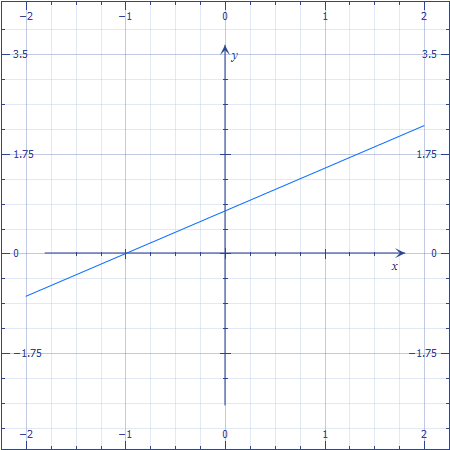
Consider this linear equation: 3x − 4y + 3 = 0
First, find the point at which the line intersects the x axis by substituting 0 for y.
3x − 4y + 3 = 0
3x − 0y + 3 = 0
3x + 3 = 0
3x + 3 − 3 = 0 − 3
3x = −3
x = −1
So when y = 0, x = −1
Next, find the point at which the line intersects the y axis by substituting 0 for x.
3x − 4y + 3 = 0
0x − 4y + 3 = 0
−4y + 3 = 0
−4y + 3 − 3 = 0 − 3
−4y = −3
\(y = \frac{3}{4}\)
We know both the x and y intercepts at this point.
So, we can plot the linear equation as shown below:
We look at linear equations in more depth in our posts on graphing.