The Square Root on Your Algebra Exam
There will be several questions on the square root on your algebra test.
Square roots are written with the radical symbol.
SQUARE ROOT EXERCISES
Instructions: Solve the problems that follow without using the square root calculator.1) \(\sqrt{196} = \text ?\)
2) \(\sqrt{121} = \text ?\)
3) \(\sqrt{225} = \text ?\)
4) Express as a decimal number:
\(\sqrt{400} + \frac{10}{\sqrt{400}}= \text ?\)
5) \(\sqrt{3.24} = \text ?\)
6) \(\sqrt{82}\) lies between which set of integers?
A. 6 and 7
B. 7 and 8
C. 8 and 9
D. 9 and 10
7) \(\sqrt{35}\) lies between which set of integers?A. 4 and 5
B. 5 and 6
C. 6 and 7
D. 7 and 8
8) Approximate \(\sqrt{164}\) to one decimal place.9) \(– \sqrt{25} = \text ?\)
10) \(\sqrt{-5} = \text ?\)
Square Roots – Answers
Answer to question 1
1) The correct answer is: 14196 is a perfect square:
\(\sqrt{196} = 14\)
Answer to question 2
2) The correct answer is: 11121 is a perfect square:
\(\sqrt{121} = 11\)
Answer to question 3
3) The correct answer is: 15225 is another perfect square:
\(\sqrt{225} = 15\)
Answer to question 4
4) The correct answer is: 20.5We need to express our result as a decimal number.
First of all, find the square root.
\(\sqrt{400} = 20\)
Then, substitute the values.
\(\sqrt{400} + \frac{10}{\sqrt{400}}= \)
\(\text 20 + \frac{10}{20}= \)
\(\text 20 + \frac{1}{2}\)
Finally, express the fraction as a decimal to solve.
\(\text 20 + \frac{1}{2} = 20.5\)
Answer to question 5
5) The correct answer is: 1.8We know that \(\sqrt{324} = 18\).
So, move the decimal place to solve.
\(\sqrt{3.24} = 1.8\)
Answer to question 6
6) The correct answer is: D\(\sqrt{81} = 9\) and \(\sqrt{100} = 10\)
82 lies between 81 and 100.
So, \(\sqrt{82}\) lies between 9 and 10.
Answer to question 7
7) The correct answer is: B\(\sqrt{25} = 5\) and \(\sqrt{36} = 6\)
35 lies between 25 and 36.
So, \(\sqrt{35}\) lies between 5 and 6.
Answer to question 8
8) The correct answer is: 12.8We have to approximate \(\sqrt{164}\) to one decimal place.
For the approximation method, remember the square roots from the chart and think of the nearest ones.
The square root of 169 is 13, so the square root of 164 will be very close to the square root of 169.
Try from 12.9 and work downwards.
12.9 × 12.9 = 166.4
12.8 × 12.8 = 163.8
12.7 × 12.7 = 161.3
163.8 is the closest to 164, so the answer is 12.8.
Answer to question 9
9) The correct answer is: –5The negative sign is outside the square root symbol.
So, first of all find \(\sqrt{25}\).
We know from our chart that \(\sqrt{25} = 5\)
To solve, we add the negative sign: –5
Answer to question 10
10) The correct answer is: an imaginary numberWe cannot multiply any real number by itself to get a negative number.
So, \(\sqrt{-5} = i\)
Square and Square Roots
To square a number, we multiply that number by itself.
A number squared uses the exponent 2.
So, a square looks like this: 42
A square root is a number that we multiply by itself to get the result specified inside the square root symbol.
The square root symbol is: \(\sqrt{16}\)
When we multiply 4 by itself, we get 16.
So, 4 is the square root of 16.
Mathematically, this is represented as:
\(\sqrt{16} = 4\)
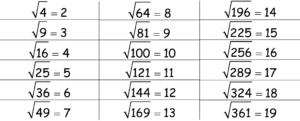
Square Roots – Chart
You should study the square roots in the chart below before you take your exam.
After you have learned the following square roots by heart, try the practice exercises in the second-to-last section of this post.
Estimating Square Roots
The square roots in the chart in the previous section are known as square roots of perfect squares.
In other words, the square roots of the numbers in the chart above are whole numbers.
You might need to use the “approximation method” for square roots that are not whole numbers.
For the approximation method, remember the square roots from the chart above and then try to think of the nearest one.
Look at the example below.
Example: Estimate to one decimal place \(\sqrt{24}\)
Answer: 4.9
We know that the square root of 25 is 5, so the square root of 24 will be very close to the square root of 25.
Try from 4.9 and work downwards.
4.9 × 4.9 = 24.01
4.8 × 4.8 = 23.04
24.01 is closer to 24 than 23.04.
So, 4.9 is the correct answer.
Square Root Calculator
On your exam, you will need to know most of the square roots for perfect squares by heart.
So, we suggest memorizing the square roots in the chart in the section above.
If you need to find square roots for a decimal number or for advanced problems on square roots, you may want to use the square root calculator.
To use the calculator, please click on the link below.
Further Algebra Practice
For further algebra practice, see our posts on decimals, fractions, and exponents.
You may also want to see our posts on radicals and imaginary numbers.