What are Sine, Cosine & Tangent?
Sine, cosine, and tangent are three ratios of the lengths of the sides of a triangle.
Since they are ratios, sine, cosine, and tangent are mathematical relationships that can be expressed as fractions.
Sine, Cosine, Tangent and the Three Sides
The measurement of sine, cosine, and tangent will depend upon which angle is being measured in the triangle.
The three sides of a right triangle are the hypotenuse, the opposite side, and the adjacent side.
Example 1:
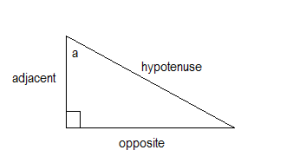
Look at the following triangle as an example:
In the triangle above, we are measuring angle “a” at the top of the triangle.
The adjacent angle is always the side of the triangle that is next to the angle being measured.
So, the left-hand side of the triangle is the adjacent side in this example.
The opposite side of the triangle is the side of the triangle across from the angle that is being measured.
So, the bottom side of the triangle is the opposite side in the triangle above.
Example 2:
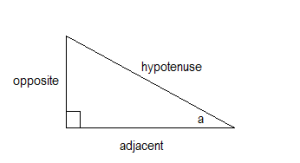
Let’s mix things up a bit and measure a different angle in the triangle.
In the triangle above, we are going to measure the angle at the side of the triangle, instead of the angle at the top of the triangle.
When you measure a different angle in the triangle, the sides that are considered to be opposite and adjacent will also change
So, the left-hand side of the triangle is now the opposite side since it is across from angle “a” in the triangle in example 2.
The bottom of the triangle is now the adjacent side since it it beside angle “a” in example 2.
Sine, Cosine & Tangent – The Ratios
Sine is the ratio that is calculated by dividing the length of the opposite side by the length of the hypotenuse.
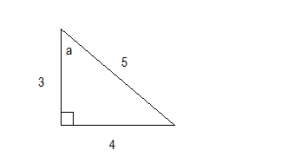
Calculating Sine – Illustrated Problem
\(\text{sine} = \frac{opposite}{hypotenuse}\)
So, the sine for the above triangle is determined as follows:
\(\text{sine} = \frac{opposite}{hypotenuse} = \frac{4}{5}\)
Calculating Cosine – Illustrated Problem
Cosine is the ratio that is calculated by dividing the length of the adjacent side by the length of the hypotenuse.
\(\text{cosine} = \frac{adjacent}{hypotenuse}\)
So, the cosine for the above triangle is determined as follows:
\(\text{cosine} = \frac{adjacent}{hypotenuse} = \frac{3}{5}\)
Calculating Tangent – Illustrated Problem
Tangent is the ratio that is calculated by dividing the length of the opposite side by the length of the adjacent side.
\(\text{tangent} = \frac{opposite}{adjacent}\)
So, the tangent for the above triangle is determined as follows:
\(\text{tangent} = \frac{opposite}{adjacent} = \frac{4}{3}\)