Number Line Examples Page
This page has number line examples and exercises for positive and negative number line problems like you will see on your exam.
What are Number Lines?
Number lines can be used to represent inequalities. So, number lines can be drawn from mathematical inequalities. Alternatively, you can determine inequalities from number lines.
When graphing inequalities, you will have to understand positive and negative number line principles.
Positive and Negative Number Line Exercises
1) Represent the solution to the following on a number line:3x < –6
2) Represent the solution to the following on a number line:–5x – 7 = 3x + 17
3) Represent the solution to the following on a number line:–7 < x = 2
4) What inequality is represented on the following number line?
5) What inequality is represented on the following number line?
Number Lines – Answers
1) Solve for x first. 3x > –6 3x ÷ 3 > –6 ÷ 3 x > –6 ÷ 3 x > –2 Then represent the result on a number line. You need to use an open dot because you do not have the equals to sign. We have the “greater than” symbol, so the line needs to point to the right.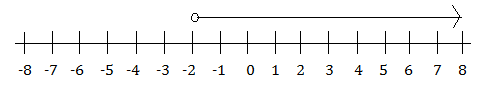
2) Solve for x first.
–5x – 7 = 3x + 17
–5x – 7 + 7 = 3x + 17 + 7
–5x = 3x + 17 + 7
–5x = 3x + 24
–5x – 3x = 3x – 3x + 24
–5x – 3x = 24
–8x = 24
–8x ÷ –8 = 24 ÷ –8
x = 24 ÷ –8 We reverse the sign when we divide by a negative.
x = –3
Then represent the result on a number line.
We need to use a solid dot because we have the “less than or equals to” sign.
We have the “less than” symbol, so the line needs to point to the left.
3) Our inequality was: –7 < x = 2
Here we have two values, so the line will not have an arrow on the end of it.
One value has the equals to sign, so we need a solid dot for the 2.
The other value does not have the equals to sign, so we need an open dot for the –7.
The value of x is in the middle, so we need to use a number line to connect the two values as show below.
4) The answer is: x = 4
Our number line was:
The line points to the left so, we need the less than sign.
We also need the equals to sign because the dot is solid.
We have the value of 4, so the answer is x = 4.
5) The answer is: –3 < x = 5
Our number line was:
We have two values, so the line will not have an arrow on the end of it.
We have a solid dot for the 5, so this value has the equals to sign.
The other value has an open dot, so it does not need the equals to sign.
So, the answer is –3 < x = 5.
Number Line Examples – 1
In this example, we will look at how to show the solution to an inequality on a number line
The most important thing to remember when working with number lines is the following:
If you multiply or divide by a negative number in an inequality, you must reverse the direction that the inequality sign points.
Now look at the two examples below before you try the practice problems.
Example: Represent the solution to the following on a number line.
25 ≥ –5x
STEP 1: Begin to solve the inequality by using inverse operations.
We have to divide by a negative number in this example, so we need to reverse the sign from “greater than or equal to” to “less than or equal to.”
25 ≥ –5x
25 ÷ –5 ≥ –5 ÷ –5 x
25 ÷ –5 ≤ x
STEP 2: Perform the operation to solve.
25 ÷ –5 ≤ x
–5 ≤ x
x ≥ –5
STEP 3: Set up a number line for the solution.
STEP 4: Represent the solution on your number line.
For “greater than or equal to” or “less than or equal to” questions, you need to use a solid dot to include the point.
So, we need to place a solid dot on –5.
Then, determine if the line should point to the left (negative) or to the right (positive).
We know that positive numbers are greater than negative numbers, so point the line toward the positive numbers, which are on the right.
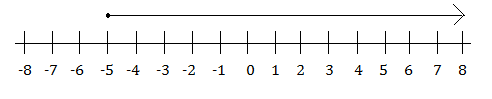
As you will see in the next example, if the sign is "greater than" or "less than" (without the "equals to"), you need to use an open circle as the dot to exclude the point.
Number Line Examples - 2
Let's look at an example of how to write inequalities from number lines.
Example: What inequality is represented on the following number line?
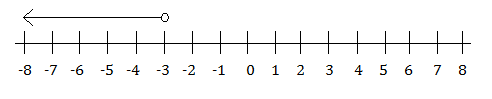
Answer: x < –3
STEP 1: Determine the value or values to be used in your inequality.
Our number line begins on –3, so we need to use the value of –3 in our inequality.
STEP 2: Determine if you should use the "greater than" or "less than" symbol or the "greater than or equal to" or "less than or equal to" symbol.
Here, we have an open dot, so we need to use either the "greater than" or "less than" symbol.
The line is pointing to the left, so we know that we need to use the "less than" symbol.
So, our answer is x < –3.
If the line had been pointing to the right, we would have needed to use the "greater than" symbol.
Further Exercises
You may wish to see our post on inequalities before you attempt the exercises in the previous section.
You can also view our posts on interval notation and graphing.
