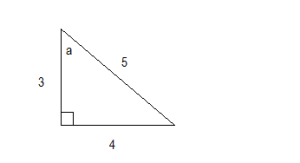
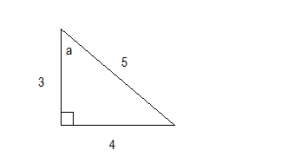
Inverse of Sin, Cos & Tan and Their Domains

In this section, we provide a basic overview of the inverse of sin, cos, and tan. We will look at these inverse trig functions and their domains.

Inverse of Sin, Cos & Tan – Quiz

Instructions: Answer the following questions on the inverse of sin, cos and tan. You may wish to study the examples below the quiz first.

[WpProQuiz 38]

Inverse of Sine

The inverse trig function for Sine is Arcsin.

Arcsin is also referred to as Sin^–1 x.

The domain for Sin^–1 x is from –1 to 1.

Inverse of Cosine

The inverse trig function for Cosine is Arccos.

Arccos is also referred to as Cos^–1 x

The domain for Cos^–1 x is also from –1 to 1.

Inverse of Tangent

The inverse trig function for Tangent is Arctan.

Arctan is also referred to as Tan^–1 x.

The domain for Tan^–1 x is all real numbers, negative infinity to positive infinity.

Inverse of Cotangent

The inverse trig function for Cotangent is Arccot.

Arccot is also referred to as Cot^–1 x.

The domain for Cot^–1 x is also all real numbers.

Inverse of Secant

The inverse trig function for Secant is Arcsec.

Arcsec is also referred to as Sec^–1 x.

The domain for Sec^–1 x is all real numbers from 1 and higher and from –1 and lower.

Inverse of Cosecant

The inverse trig function for Cosecant is Arccsc.

Arccsc is also referred to as Csc^–1x.

The domain for Csc^–1x is like that for the inverse Secant function, so it is all real numbers from 1 and higher and from –1 and lower.

Ned to Review Basic Trig Functions?

If you need to review basic functions before completing the exercises on this page, please see our posts entitled Function Notation and Inverse Functions.

Working with Inverse Trig Functions

Be careful with inverse trig functions. Using -1 for the exponent means an inverse function, not raising the function to the -1 power.

The best way to do calculations involving inverse trig functions is to use a good trigonometry calculator.

Trigonometry calculators can be found online at:

Free Trigonometry Calculator for 12 Trig Identities

Free Trigonometry Calculator for Trig Functions

However, in order to use the online inverse trig functions wisely, you should first have a good grasp of how to change a function’s reciprocal.

Example:

For example: Cot^–1 (2) = Tan^–1 (1/2)

Cot^–1, also called Arccot, is the inverse of Tan^–1, also called Arctan.

We need to reverse the position of the numerator and denominator in the Cot^–1 part of the equation to get the Tan^–1 part of the equation.

2 is equal to the fraction 2/1, so we flip this in the inverse function to become 1/2.

More trigonometry practice

Get the download

Fundamental Trig Identities Page

There are three fundamental trig identities: sine, cosine, and tangent.

There are three reciprocal trig identities: secant, cosecant, and cotangent.

Sine, Cosine & Tangent

You will remember that the formulas for the three basic trig identities are:

\(\text{sine} = \frac{opposite}{hypotenuse}\)

\(\text{cosine} = \frac{adjacent}{hypotenuse}\)

\(\text{tangent} = \frac{opposite}{adjacent}\)

Cosecant, Secant and Cotangent

You will remember that the formulas for the three inverse trig identities are:

\(\text{cosecant} = \frac{hypotenuse}{opposite}\)

\(\text{secant} = \frac{hypotenuse}{adjacent}\)

\(\text{cotangent} = \frac{adjacent}{opposite}\)

Fundamental Trig Identities Quiz

Instructions: Use your knowledge of trig identities to answer the following questions. Then check your answers in the next section.

Triangle XYZ above is a 30-60-90 degree triangle.

Angle X measures 60 degrees.

Side XY is a units in length.

Side YZ is a√3 units in length.

Side XZ is 2a units in length.

Question 1:  The cosecant of angle X is 2/√3. What is the sine?

Question 2:  The secant of angle X is 2 . What is the cosine?

Question 3:  The cotangent of angle X is 1/√3. What is the tangent?

Question 4:  If tan² X = 3, what is sec²?

Question 5:  Prove that sin X × csc X = 1

Trig Identities – Answers

Answer 1:

\(\text{The reciprocal of cosecant is sine} = \frac{1}{csc A} = \text{sin A}\)

So, if the cosecant of angle X is 2/√3 , the sine is √3/2.

Answer 2:

\(\text{The reciprocal of secant is cosine} = \frac{1}{sec A} = \text{cos A}\)

So, if the secant of angle X is 2, the cosine is 1/2.

Answer 3:

\(\text{The reciprocal of cotangent is tangent} = \frac{1}{cot A} = \text{tan A}\)

So, if the cotangent of angle X is 1/√3, the tangent is √3.

Answer 4:

If tan² X = 3, what is sec²?

tan² X + 1 = sec² X

3 + 1 = sec²

sec² = 4

Answer 5:

Prove that sin X × csc X = 1

Here, we have a 30-60-90 degree triangle and the relative lengths of the sides are provided in the facts of the problem.

The sine of X is therefore  is √3/2 and the cosecant is 2/√3 .

Proof:  √3/2  × 2/√3 = 2√3/2√3 = 1

Trig Identities – Abbreviations

The following abbreviations are commonly used when discussing trigonometric identities:

• sin = sine
• cos = cosine
• tan = tangent
• csc = cosecant
• sec = secant
• cot = cotangent

The abbreviation may also be used with the identity of the angle to which it relates, such as csc α or cot λ.

Reciprocal Identities – Defined

Secant is the reverse of cosine.

Cosecant is the reverse of sine.

Cotangent is the reverse of tangent.

We can express these identities as fractions that contain 1 in the numerator as shown below:

Cosecant (CSC)

\(\text{The reciprocal of sine is cosecant} = \frac{1}{sin A} = \text{csc A}\)

Secant (Sec)

\(\text{The reciprocal of cosine is secant} = \frac{1}{cos A} = \text{sec A}\)

Cotangent (Cot)

\(\text{The reciprocal of tangent is cotangent} = \frac{1}{tan A} = \text{cot A}\)

Sine (Sin)

\(\text{The reciprocal of cosecant is sine} = \frac{1}{csc A} = \text{sin A}\)

Cosine (Cos)

\(\text{The reciprocal of secant is cosine} = \frac{1}{sec A} = \text{cos A}\)

Tangent (Tan)

\(\text{The reciprocal of cotangent is tangent} = \frac{1}{cot A} = \text{tan A}\)

Reciprocal Identities – Proof

When working out problems on trig identities, you may need to do a proof.

“Doing a proof” means that you need to check your work, using a different formula.

Fundamental Trig Identities – Proofs

In order to prove trig identities, remember the following equations:

sin Α × csc A = 1

cos A × sec A = 1

tan A × cot A = 1

Pythagorean Identities

Pythagorean identities are useful in order to manipulate equations and expressions.

Here are some of the most important trigonometric Pythagorean identities:

sin² A + cos² A = 1

tan² A + 1 = sec² A

1 + cot² A = csc² A

Trig Identities – Differing Notations

You might see different notations when calculating the square of the trig identities.

For ease of reference, the parentheses in trig identities are sometimes removed.

For instance, sin² A is the same as (sin A)² and tan² A is the same as (tan A)².

You may also want to have a look at the following posts:

Sine, Cosine & Tangent

Trigonometric Functions

Algebra Problems

Geometry Questions

Purpose of Trigonometric Functions

Trigonometric functions help us to understand relationships of the measurements of the sides of triangles to one another.

They can also help us to understand the relationships between measurements of other geometric shapes, such as chords and circles.

Trigonometric functions are essentially ratios containing the numbers or variables that represent these measurements.

If you are going to study engineering, trigonometric functions will help you to construct models.

You will also need to know trigonometric functions if you are taking an entrance exam that has a calculus component.

Trigonometric Functions – The Basic Concepts

Before we begin to talk about the six trigonometric functions, you should refer back to our post entitled “Sine Cosine Tangent.”

From that post, you will need to remember that the three sides of a triangle are the hypotenuse, the opposite side, and the adjacent side.

You will also remember from that post that three of the trig functions are sine, cosine, and tangent.

\(\text{sine} = \frac{opposite}{hypotenuse}\)

\(\text{cosine} = \frac{adjacent}{hypotenuse}\)

\(\text{tangent} = \frac{opposite}{adjacent}\)

Some students remember these trig functions by using the first letters of each of the equations:

SOH

CAH

TOA

Other students try to remember the basic functions as one word: SohCahToa

The Six Trigonometric Functions – Example

Having reviewed the basics, now let’s look at an example:

In our example triangle above, the side that measures 4 is the opposite side because it is across from angle a, which is the angle being measured.

The side that measures 3 is the adjacent side because it is next to angle a.

The side that measures 5 is the hypotenuse, because it is across from the right angle.

So, if we have a triangle with sides that measure 3, 4 and 5, we can form six different ratios.

Using the measurements of the sides with their descriptions, we get our six trigonometric functions:

\(\text{cosine} = \frac{3}{5} = \frac{adjacent}{hypotenuse}\)

\(\text{tangent} = \frac{4}{3} = \frac{opposite}{adjacent}\)

\(\text{sine} = \frac{4}{5} = \frac{opposite}{hypotenuse}\)

\(\text{secant} = \frac{5}{3} = \frac{hypotenuse}{adjacent}\)

\(\text{cosecant} = \frac{5}{4} = \frac{hypotenuse}{opposite}\)

\(\text{cotangent} = \frac{3}{4} = \frac{adjacent}{opposite}\)

The Reciprocal Trigonometric Functions

The secant, cosecant, and cotangent functions are called the reciprocal functions.

They are referred to as reciprocal because they flip the ratios of sine, cosine, and tangent.

“Flipping” the ratio means that they swap the position of the numerator and denominator in the particular ratio.

In other words, secant is cosine upside-down:

\(\text{secant} = \frac{hypotenuse}{adjacent}\)

Cosecant is sine upside-down:

\(\text{cosecant} = \frac{hypotenuse}{opposite}\)

Cotangent is tangent upside-down:

\(\text{cotangent} = \frac{adjacent}{opposite}\)

Further Problems on Trig Functions

As you can see, you can easily solve the reciprocal function if you have the values for its basic function.

Trigonometric identities are the relationships between the basic functions and the reciprocal functions.

Please see our post on Trigonometric Identities for further practice with trig functions.

What are Sine, Cosine & Tangent?

Sine, cosine, and tangent are three ratios of the lengths of the sides of a triangle.

Since they are ratios, sine, cosine, and tangent are mathematical relationships that can be expressed as fractions.

Sine, Cosine, Tangent and the Three Sides

The measurement of sine, cosine, and tangent will depend upon which angle is being measured in the triangle.

The three sides of a right triangle are the hypotenuse, the opposite side, and the adjacent side.

Example 1:

Look at the following triangle as an example:

In the triangle above, we are measuring angle “a” at the top of the triangle.

The adjacent angle is always the side of the triangle that is next to the angle being measured.

So, the left-hand side of the triangle is the adjacent side in this example.

The opposite side of the triangle is the side of the triangle across from the angle that is being measured.

So, the bottom side of the triangle is the opposite side in the triangle above.

Example 2:

Let’s mix things up a bit and measure a different angle in the triangle.

In the triangle above, we are going to measure the angle at the side of the triangle, instead of the angle at the top of the triangle.

When you measure a different angle in the triangle, the sides that are considered to be opposite and adjacent will also change

So, the left-hand side of the triangle is now the opposite side since it is across from angle “a” in the triangle in example 2.

The bottom of the triangle is now the adjacent side since it it beside angle “a” in example 2.

Sine, Cosine & Tangent – The Ratios

Sine is the ratio that is calculated by dividing the length of the opposite side by the length of the hypotenuse.

Calculating Sine – Illustrated Problem

\(\text{sine} = \frac{opposite}{hypotenuse}\)

So, the sine for the above triangle is determined as follows:

\(\text{sine} = \frac{opposite}{hypotenuse} = \frac{4}{5}\)

Calculating Cosine – Illustrated Problem

Cosine is the ratio that is calculated by dividing the length of the adjacent side by the length of the hypotenuse.

\(\text{cosine} = \frac{adjacent}{hypotenuse}\)

So, the cosine for the above triangle is determined as follows:

\(\text{cosine} = \frac{adjacent}{hypotenuse} = \frac{3}{5}\)

Calculating Tangent – Illustrated Problem

Tangent is the ratio that is calculated by dividing the length of the opposite side by the length of the adjacent side.

\(\text{tangent} = \frac{opposite}{adjacent}\)

So, the tangent for the above triangle is determined as follows:

\(\text{tangent} = \frac{opposite}{adjacent} = \frac{4}{3}\)

GEOMETRY PRACTICE TEST QUESTIONS