Category: Geometry

The Distance Around a Circle is Called Circumference

The distance around the outside of the circle is called the circumference.

Distance Around a Circle – Circumference Quiz

Instructions: Calculate the distance around a circle in the exercises that follow. You may want to see the formulas and examples in the next section first.

[WpProQuiz 36]

Circumference – Illustrated

Look at the illustration of a circle below:

The distance of the black line around the outside of a circle like the one above is its circumference.

Formula for Circumference of a Circle

You will need to remember the symbol π when using the formula for circumference of a circle.

Circumference = 2πr

The radius of the circle is represented by r in the above formula.

What is the Radius?

The radius is the measurement from the center of a circle to the outside edge of the circle.

The circle below illustrates a radius:

Circumference with Diameter

Since the radius of the circle is half of the diameter, you can also use this formula for circumference of a circle:

Circumference = πd

The diameter of the circle is represented by d in the above formula.

Questions on the Circumference of a Circle

Values for π

You can sometimes express circumference as a number and the π symbol.

Other times, you may be asked to use a value for π, such as 3.14

Practical Problems

Some questions on the circumference of a circle may also involve practical situations, like measuring the distance around the outside of a wheel or other circular object.

Difference in Circumference

You may also see questions that ask you to find the difference between the circumferences of two circles.

Other Aspects of Circles

Area

Area is a measurement of the space on the inside of a circle.

Chords

Chords are lines that are drawn between two points on the outside of a circle.

Arcs

An arc is a part of the circumference of a circle.

Semicircles

A semicircle is half of a circle. You will need to understand semicircles for problems on hybrid shapes.

We will look at area, chords, arcs, and hybrid shapes in separate posts.

Free Geometry Review

Exam SAM on YouTube

Surface Area of Triangle Formula

The surface area of a triangle formula is: ¹/₂ × base × height.

The formula can also be expressed as:

In the formula above, A is the area of the triangle, b is the base, and h is the height.

Area of a Triangle – Quiz

[WpProQuiz 35]

The examples that follow illustrate how to use the formula.

Surface Area of a Triangle Formula – Example

In exam questions on triangles, you may see illustrations of triangles.

Alternatively, the facts and measurements of the figure may be given in narrative form, without an illustration.

For example, you might see a figure like the one below:

On the other hand, the question may be presented in narrative form.

Example: What is the area of a triangle with a height of 7 units and a base of 5 units?

Answer: The answer to the question is an area of 17.5 square units.

To solve the problem, we need to use the area of a triangle formula provided above.

Area of a triangle formula = ¹/₂ × base × height

Then substitute the values stated in the question.

¹/₂ × 5 × 7 =

¹/₂ × 35 =

17.5

Triangles and Other Shapes

Exam questions may cover triangles that lie inside other shapes.

These types of exam questions will often show a triangle or triangles inside a rectangle.

Triangles can also be added to the sides of a rectangle to form a trapezoid.

Two congruent triangles can be joined at the base to form a parallelogram.

Look at the illustration below:

So, you might also see questions on parallelograms and trapezoids on the exam.

You may also want to try our other free geometry questions.

Get the downloads

Area of a Square Formula with Example

This page provides the area of a square formula, with an example for you to study.

Area of Square Formula

Many entrance exams will ask you to solve problems on the area of a square. 

In the formula below, L is the length of the side and A is the area. 

The formula for the area of a square is:  L² = A

Area of a Square – Quiz

Now try the quiz below:

[WpProQuiz 34]

Avoiding Common Mistakes

You will remember that a square has four sides that are equal in length.

You should be careful not to use the formula for the perimeter of a square if you really want to calculate the area instead.

Calculating Square Footage

You may be asked to determine square footage on your exam.

Exam problems on square footage may involve squares, rectangles, or hybrid shapes.

The formula for square footage is:

L × W = square footage

L is the length of the space and W is the width.

The result will be expressed in square feet.

Width Equals Length

Of course, for problems involving squares, the length and width will be equal.

Perimeter and other concepts

You may want to have a look at our post on the perimeter of a square after completing the exercises on this page.

For example, consider the following sample question:

A square room measures three feet by three feet. What is the square footage of this room?

The answer is 9 square feet.

To solve, use the formula above:

L² = A

3² = 9 square feet

You can see the answer more clearly by looking at the following diagrams:

This small square measures 1 foot long and 1 foot wide:

The large square below is 3 feet wide and 3 feet long.

We can fit nine of these small squares inside the large square.

So, the large square is 9 square feet.

You may also want to look at our other geometry exam problems.

Get the Downloads

Calculate Surface Area of a Circle Given Radius or Diameter

This page will show you how to calculate the surface area of a circle given radius or diameter.

Study the examples in the sections below before doing the quiz.

Surface Area of a Circle – Quiz

Instructions: Calculate the areas of the circles in each question that follows.

[WpProQuiz 33]

What is Surface Area?

The surface area of a circle is the amount of space on the inside of the circle.

Look at the illustration of a circle below:

The amount of space in the blue part of the circle is the surface area of the circle.

Formula for Area with Radius

The area of a circle is calculated by using π.

The formula for the area of a circle with the radius is as follows:

Area of a circle = πr²

Formula for Area with Diameter

Remember that radius is half of diameter.

So, for the area of a circle given diameter, use this formula:

Area of a circle = π × (D × ¹/₂)²

Values of π

π is equal to approximately 3.14.

However, you may see other more precise values for π, such as 3.142 or 3.14159.

Questions on Your Exams

Calculation with values

You may have to calculate the area of a circle based on the values provided.

Illustrations

You may also see questions asking you to study an illustration, and then calculate the area of a circle based on the illustration.

Differences of Areas

Exam questions also involve calculating the difference between the areas of two circles.

Practical Problems

There will also be practical questions about determining the area of circular objects.

Area of a Circle – Example Problems

Determine the answers to the following questions based on the facts provided.

Problem 1:

What is the area of a circle that has a radius of 8?

Problem 2:

What is the difference between the areas of the circles in the following diagrams?

Problem 3:

The city is going to build a pond in the local park.

The pond will have a walking path around it as shown in the grey part of the following diagram.

The walking path will be paved with a substance that costs $500 per square meter.

How much will it cost to pave the path? Use 3.14 for π.

Answers to the Area of a Circle Problems

Answer 1:

What is the area of a circle that has a radius of 8?

Use the formula provided above to solve the problem.

Area of a circle = πr²= π8² = 64π

Answer 2:

Here are the circles again.

First, calculate the area for each circle.

Area of circle A= πr²= π10² = 100π

Area of circle B = πr²= π12² = 144π

Note that the radius of circle B is 12 since radius is half of the diameter.

Then, subtract the area of the circle A from the area of circle B.

144π – 100π = 44π

Answer 3:

First, we need to find the difference between the area of pond and the area including the path and the pond.

Area of pond = πr²= 2.5 × 2.5 × 3.14 = 19.625 square meters

Area of a pond and path= πr²= 3.5 × 3.5 × 3.14 = 38.465 square meters

Then, subtract to find the area of path.

Area of path = 38.465 – 19.625 = 18.84 square meters

Finally, multiply by the cost per square meter in order to get the total cost.

Cost = 18.84 square meters × $500 per square meter = $9,420

Other Areas of Circles

What is a Sector?

A sector is a part of a circle that looks like a piece of pie.

To put it in geometric language, a sector is part of a circle enclosed between two radii.

The illustration below shows a sector:

Segments

A segment is a piece of a circle that is formed by a chord.

The top portion of the following circle is a segment:

A segment should not be confused with a semicircle.

Geometry Practice Problems

Get the downloads

What are Polygons?

Polygons are two-dimensional shapes that are made up of straight lines.

Polygons cannot have any curved sides.

Regular polygons have sides that are all of the same length.

Types of Polygons

You should know the types of special polygons for your geometry test.

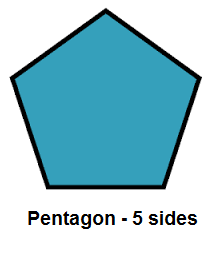
A pentagon is a polygon that has five sides:

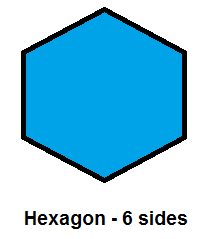
A hexagon is a polygon with six sides:

A heptagon is a polygon with seven sides:

An octagon is a polygon with eight sides:

A decagon is a polygon with ten sides:

All of the polygons in the illustrations above are regular polygons.

Each side in a regular polygon is the same length as the other sides.

Irregular polygons

In an irregular polygon, the sides are not equal in length.

Look at the sides of the polygon in the example below.

Complex polygons

In a complex polygon, the sides intersect with one another.

So, a complex polygon can look like two or more triangles that have been combined.

A complex polygon could also look like a combination of other polygons, like squares and triangles.

Concave polygons

Concave polygons have at least one angle that points towards the inside of the shape.

The internal angle of a concave polygon has to be more than 180°.

A straight line has 180°, so the concave part of the polygon has to point inwards.

Polygons and Interior Angles

You can work out the sum of the interior angles of a polygon by dividing the shape into triangles.

Draw all of your lines from the same corner (also called a vertex).

Look at how the lines are drawn in the polygon below:

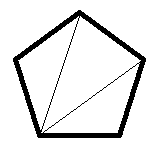
You will remember from our previous post on triangles that the sum of all of the angles inside a triangle is 180°.

STEP 1:  Determine the total measurement of the interior angles.

In our example above, we have made three triangles.

So, the sum of all of the degrees of the interior angles in our polygon is 540:

180° × 3 triangles = 540°

STEP 2:  Determine the measurement of each interior angle.

If the polygon is regular, you can divide the total degrees by the number of angles to determine the degree measurement of each angle.

We have a regular pentagon (with 5 angles) in our example above, so divide total degrees by 5 to get the measurement of each angle.

540° ÷ 5 = 108° for each interior angle

Special Polygons – Interior Angle Meaurement

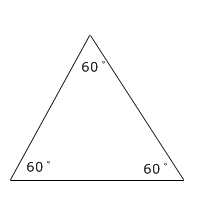
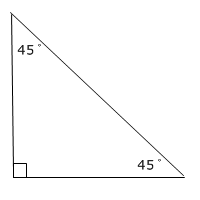
Equilateral triangle

180° ÷ 3 angles = 90° for each interior angle

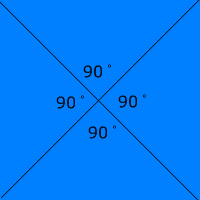
Square, rectangle, or regular quadrilateral

A square, rectangle, or other regular quadrilateral can be divided into two triangles.

This can be done by drawing a line from one corner to the opposite corner.

180° × 2 triangles = 360°

So, each angle in a square, rectangle, or regular quadrilateral has 90°.

360° ÷ 4 angles = 90° for each interior angle

Regular pentagon

A regular pentagon can be divided into three triangles.

This can be done by drawing two lines from one corner to the opposite corners.

So, the total of all of the degrees of the angles in a polygon is 540.

180° × 3 = 540°

So, each angle in a regular pentagon has  108°.

540° ÷ 5 angles = 108° for each interior angle

Regular hexagon

A regular hexagon can be divided into four triangles.

This can be done by drawing three lines from one corner to the opposite corners.

So, the total of all of the degrees of the angles in a polygon is 720.

180° × 4 = 720°

So, each angle in a regular hexagon has  120°.

720° ÷ 6 angles = 120° for each interior angle

Interior Angles in Other Polygons

To determine the size of any interior angle of a regular polygon, follow these steps:

• Divide the polygon into triangles drawing lines from one corner to the opposite corners.
• Count how may triangles you have made.
• Multiply the number of triangles by 180 to get the total degrees for all interior angles.
• Divide the total degrees by the number of angles to determine the measurement of each interior angle.

Polygons and Exterior Angles

To determine the size of any exterior angle in a polygon, draw a straight line from the corner.

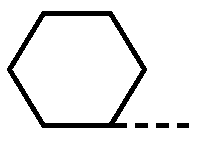
Here we have a regular hexagon, so each interior angle has 120°.

A straight line has 180°, so we subtract to find the measurement of the exterior angle.

180° – 120° = 60°

So, the exterior angle in the hexagon above is 60°.

Further Geometry Practice

You may also want to view the following posts:

Triangles

Circles

Squares and Rectangles

Exam Questions on Types of Triangles

You will need to know the different types of triangles for your entrance exam.

Your should also understand some basic rules about the types of triangles.

Types of Triangles – Definitions

Isosceles

An isosceles triangle has two equal sides and two equal angles.

An example of an isosceles triangle is shown below:

Equilateral

An equilateral triangle has three equal sides and three equal angles.

The illustration below shows an equilateral triangle:

Congruent

Equilateral triangles are sometimes called congruent triangles.

That is because angles that have the same measurement in degrees are called congruent angles.

Obtuse

An obtuse triangle has one angle that is greater than 90 degrees.

So, an obtuse triangle can look something like the following illustration:

30 – 60 – 90 Triangle

The sum of all three angles in any triangle must be equal to 180 degrees.

This is true in a 30 – 60 – 90 triangle because 30 + 60 + 90 = 180.

The sides of a 30° – 60° – 90° triangle are in the following ratio:  1: √3 : 2

45 – 45 – 90 Triangle

Remember that the sum of all three angles in any triangle must be equal to 180 degrees, so in this type of triangle:  45 + 45 + 90 = 180

You may also want to see our posts on the the area of a triangle and the area of a square.

Free Geometry Practice

Formula for the Perimeter of a Square

You will need to know how to calculate the perimeter of a square for your entrance exam.

The formula for the perimeter of a square is:

4 × L = P

In the formula above, L is the length of the side of the square and P is the perimeter of the square.

To understand exam questions on the perimeter of a square, you should know some facts about squares.

You should also understand the terminology relating to squares and other geometrical shapes.

You may want to have a look at our post on the area of a square after completing the exercises on this page.

Perimeter of a Square – Terminology

Quadrilateral:

A square is a type of quadrilateral.

“Quadrilateral” means that the shape has four sides.

Symmetry:

A square is said to have four lines of symmetry.

This means that a square has four sides, and all four sides are equal in length.

Rotational symmetry:

A square also has rotational symmetry.

This means that the square will look the same, regardless of how it is rotated.

So, you can turn a square on its side and it will look the same.

90° angles:

All angles in a square are 90 degrees.

Since all four angles are 90 degrees, a square is different than a polygon or hybrid shape.

Parallel lines:

A square has two pairs of parallel lines.

The left and right sides of the square will be parallel.

The top and bottom sides of the square will also be parallel.

Bisecting angles:

The diagonals in a square are equal.

The diagonals bisect, or cross each other, in the center of the square.

The diagonal lines form four right angles.

You will need to know these facts when working out other geometry problems on the exam.