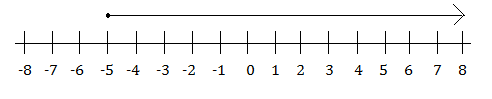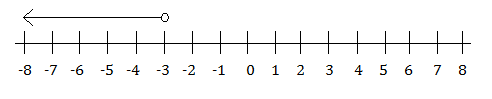Category: Algebra

What is Interval Notation for Inequalities?

You will need to learn which symbols to use to express interval notation for inequalities, including the infinity symbol.

On your exam, you may need to express an inequality or number line in interval notation.

Interval Notation for Inequalities – Quiz

Instructions: Answer the questions in the quiz that follows. You should view the interval notation example problems in the next section first.

[WpProQuiz 37]

Interval Notation – How to Use the Symbols

We use the following symbols for interval notation:

Greater than and less than

We use the symbols (  ) and  [   ] in interval notation.

[     and    ]    →     use for  ≤  or   ≥

(    and     )    →     use for  <  or   >

Infinity

∞       →     use for infinity

–∞     →     use for negative infinity

Solid dots

Solid dots on a number line are for  ≤  and  ≥,  so when you see

solid dots   →   use  [   or  ]

Open dots

Open dots on a number line are for  <  and  >,  so when you see

open dots  →   use  (   or   )

You also need to use (   or   ) next to the infinity symbol.

Whether we use the opening bracket or parenthesis, or alternatively the closing bracket or parenthesis, depends on the position of x.

Interval Notation Examples

Let's look at some examples of how to write inequalities in interval notation.

You will notice that the numbers and symbols in interval notation are written in the same order as a number line.

So, the lowest value for the inequality is placed on the left side in each set of parentheses or brackets.

Example 1:

x > 9 is written as (9 , ∞)

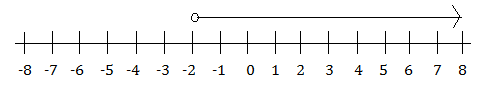
The number line for the notation in example 1 would show an open dot on 9 and a line with an arrow on the end of it, going from the dot to the right towards infinity.

Example 2:

x < 10 is written as (–∞, 10)

The number line for the notation in example 2 would show an open dot on 10 and a line with an arrow on the end of it, going from the dot to the left towards the negative numbers and negative infinity.

Example 3:

x ≥ 8 is written as [8 , ∞)

The number line for the notation in example 3 would show an solid dot on 8 and a line with an arrow on the end of it, going from the dot to the right towards infinity.

Example 4:

x ≤ –7  is written as (–∞, –7]

The number line for the notation in example 4 would show an solid dot on –7 and a line with an arrow on the end of it, going from the dot to the left towards the negative numbers and negative infinity.

Example 5:

–3 ≤ x ≤ 6 is written as [–3 , 6]

The number line for the notation in example 5 would show a solid dot on –3 on the left and another solid dot on 6 at the right, with a line going between them.

Example 6:

–2 < x ≤ 4 is written as (–2 , 4]

The number line for the notation in example 6 would show an open dot on –2 on the left and a solid dot on 4 at the right, with a line going between them.

Example 7:

9 < x < 12 is written as (9, 12)

The number line for the notation in example 7 would show an open dot on 9 on the left and another open dot on 12 at the right, with a line going between them.

Example 8:

–5 ≤ x < 8 is written as [–5 , 8)

The number line for the notation in example 8 would show a solid dot on –5 on the left and an open dot on 8 at the right, with a line going between them.

Using the infinity symbol

As you can see from the interval notation examples, we need to use the infinity sign when we have an inequality with only one value.

That is because for inequalities with one value and with the "greater than" symbol (such as x > 9), there are an infinite amount of positive values that are greater than 9.

Similarly, for inequalities with one value and with the "less than" symbol (such as x < 10), there are a finite amount of positive values but an infinite amount of negative values that are less than 10.

Answering Exam Questions

You may see the following types of questions on your algebra test:

Writing interval notation from inequalities or number lines

Preparing inequalities or number lines from interval notation

You may  want to see our posts on number lines and inequalities.

Further Practice

You may also want to see our posts on graphing and quadratics.

Exam SAM on YouTube

Solving Quadratic Equations by Factoring – Examples for Your Exam

You will need to study solving quadratic equations by factoring with examples in order to learn this skill for your math exam.

If you do not know how to factor, please see our post on factoring quadratics before continuing.

To see the examples, please go to the sections below the quiz.

Solving Quadratics Equations by Factoring – Quiz

Instructions:  Solve the quadratic equations provided below. Then check your answers after each question.

[WpProQuiz 29]

Solving Quadratic Equations by Factoring – Example

If the equation is not equal to zero, you will need to go about solving quadratic equations by factoring using the steps below.

Look at the following example.

Solve for a:  (a + 4)(a – 2) = 7

STEP 1: Perform the FOIL Mehtod

Perform the FOIL method on the left-hand side of the equation.

(a + 4)(a – 2) = 7

(a × a) + (a × –2) + (4 × a) + (4 × –2) = 7

a² – 2a + 4a – 8 = 7

a² + 2a – 8 = 7

STEP 2: Perform the Operations

Perform addition or subtraction to make the right-hand side of the equation zero.

a² + 2a – 8 = 7

a² + 2a – 8 – 7 = 7 – 7

a² + 2a – 15 = 0

STEP 3: Factor the New Equation

a² + 2a – 15 = 0

Look at the third term of the equation, which is –15 in our problem.

Factor the Constant

We need to find two integers that equal –15 when they are multiplied.

–1 × 15 = –15

–3 × 5 = –15

–5 × 3 = –15

–15 × 1 = –15

Factor the Coefficient

Then look at the second term of the equation.

We need to be sure that our two integers also equal 2 when they are added.

–1 + 15 = 14

–3 + 5 = 2

–5 + 3 = –2

–15 + 1 = –14

Set up the Factored Form

Finally, take the two integers that meet both conditions above, and set out the factored form of the quadratic equation.

(a – 3)(a + 5) = 0

STEP 4: Solve for the First Set of Parentheses

Solve for a in the left-hand set of parentheses in the newly factored equation.

(a – 3)(a + 5) = 0

(3 – 3) × (a + 5) = 0

(0) × (a + 5) = 0

So, 3 is a solution.

STEP 5: Solve for the Second Set of Parentheses

Solve for a in the right-hand set of parentheses in the newly factored equation..

(a – 3)(a + 5) = 0

(a – 3) × (–5 + 5) = 0

(a – 3) × (0) = 0

So, –5 is another solution.

Solving Quadratic Equations  – “Equal to Zero” Method

This method is for quadratic equations in their factored form.

Look at the following example.

Solve for x:  (x + 1)(x – 2) = 0

When solving quadratic equations, you will usually need to find two solutions for the squared variable, which is x in our problem.

Remember to solve for zero for each set of parentheses!

You will also need to be sure that the equation equals zero.

When the number to the right of the equals sign is zero, we know that one of the multipliers also needs to be zero.

STEP 1:

Solve for x in the left-hand set of parentheses.

(x + 1)(x – 2) = 0

(–1 + 1) × (x – 2) = 0

(0) × (x – 2) = 0

So, –1 is a solution.

STEP 2:

Solve for x in the right-hand set of parentheses.

(x + 1)(x – 2) = 0

(x + 1) × (2 – 2) = 0

(x + 1) × (0) = 0

So, 2 is also a solution.

Solving Quadratic Equations – Other Methods

To learn how to solve equations in the standard quadratic form, please see our posts on completing the square and the quadratic formula.

You may also want to view our posts on the quadratic equation and algebra.

Visit Us on YouTube

What is Scientific Notation with Negative Exponents?

To express a decimal in scientific notation, you need to use negative exponents and use a number between one and ten.

Scientific Notation with Negative Exponents – Example 1

For example, the number .000387 is written in scientific notation as 3.87 × 10^-4.

Determining the exponent

If your given number is a decimal, you need to move the decimal point to the right and count the number of places to the left.

You can count the decimal places to the left as shown in the illustration below:

As you can see in the illustration above, you need to use scientific notation with a negative exponent for your answer of 3.87 × 10^-4

Scientific Notation Quiz

Instructions: For questions 1 to 5, express the numbers in scientific notation, using negative exponents where necessary. For questions 6 to 10, express the numbers as integers or decimals.

[WpProQuiz 27]

What is Scientific Notation?

Scientific notation means that you express a decimal as a number between 1 and 10 multiplied by 10^m.

Example 2

In scientific notation, you need to remember to multiply by a power of 10.

For example, the number 635,000 is written in scientific notation as 6.35 × 10⁵.

Count the decimal places

The first step is to move the decimal point to the left, and then count the number of places to the right.

You can count the decimal places as shown in the illustration below:

Shortcut Method

So, the amount of decimal places that you move is the same number that you use for your exponent.

The exponent also correlates to the amount of zeroes that are to be placed after the 1 when we multiply the power of ten.

10⁵ = 10 × 10 × 10 × 10 × 10 = 100,000

In other words, 100,000 has 5 zeroes so it is equal to 10⁵.

You may need to change numbers to or from scientific notation on your exam.

Scientific Notation – Multiplication

You may see problems that involve multiplication with numbers in scientific notation.

Look at the following example:

(3 × 10²) × (2 × 10⁴) = ?

To solve multiplication problems like this one, multiply the integers first.

STep 1 – Multiply the ingeters

In our problem, the integers are 3 and 2, so do the multiplication:

3 × 2 = 6

Step 2 – Add the exponents

Then you need to remember to add the exponents when multiplying powers of 10.

So, 10² × 10⁴ = 10⁶

Step 3 – Combine for the scientific notation

Finally, put the two results together for your answer.

(3 × 10²)(2 × 10⁴) = 6 × 10⁶

Scientific Notation – Advanced Questions

Notice that you may also see multiplication problems presented like this:

(3 × 10²)(2 × 10⁴) = ?

Remember that the times sign between the parentheses is sometimes omitted.

(3 × 10²) × (2 × 10⁴) = (3 × 10²)(2 × 10⁴)

Scientific Notation – Division

You may also see problems that involve division with numbers in scientific notation.

Look at the following example:

(9 × 10⁷) ÷ (3 × 10³) = ?

Step 1 – Divide the integers

First you need to divide the integers.

9 ÷ 3 = 3

Step 2 – Subtract the exponents

When we divide powers of ten, we need to subtract the exponents.

So, 10⁷ ÷ 10³ = 10⁴

Step 3 – Combine for the Scientific Notation

Then combine the results for your answer.

(9 ÷ 10⁷)(3 ÷ 10³) =  3 × 10⁴

You may also want to visit our page on decimals and our post on exponent laws.

Free algebra test

Join Us on YouTube

Solve Multi Step Inequalities in Math

You will see various types of questions on how to solve multi step inequalities on your algebra test.

This post provides an overview of linear, absolute value, and quadratic inequalities.

Solve Multi Step Inequalities – Quiz

Instructions:  Find all possible values of x for the inequalities provided. You may want to study the examples below the quiz first.

[WpProQuiz 28]

Solve Multi Step Inequalities – Linear Inequality Example

The way we go about solving linear inequalities is very similar to the process used in solving linear equations.

You need to deal with the integers in the inequality, and then isolate the variable.

Look at the example linear inequality problem below.

Example:  Solve for possible values of x.

–3(2x + 5) > 9

Answer:  x < –4

STEP 1:  

Perform operations on the parentheses.

–3(2x + 5) > 9

–3 × (2x + 5) > 9

(–3 × 2x) + (–3 × 5) > 9

–6x + (–15) > 9

–6x – 15 > 9

STEP 2:  

Deal with the integers.

–6x – 15 > 9

–6x – 15 + 15 > 9 + 15

–6x  > 9 + 15

–6x  > 24

STEP 3:  

Isolate x to solve.

–6x  > 24

–6x  ÷ –6 > 24 ÷ –6

Remember When to Change Signs!

Remember that when you divide or multiply by a negative in an inequality, you need to change the direction of the sign.

–6x  ÷ –6 > 24 ÷ –6 We are dividing by a negative number here.

x  < 24 ÷ –6 So, now need to use the “less than” symbol.

x  < –4

Check Your Answer

You can check your work to be sure that you have the inequality sign pointing in the right direction.

We will use –5 for x in the proof below since it satisfies the statement that x  < –4.

–3(2x + 5) > 9

–3[(2 × –5) + 5] > 9

–3[(–10) + 5] > 9

(–3 × –10) + (–3 ×  5) > 9

30 – 15 > 9

15 > 9

Solving Inequalities – Absolute Value Example

Absolute value can be thought of as the distance of a number from zero on a number line.

So, absolute value is always a positive number.

Using the absolute value symbol, we can demonstrate as follows: |–5| = 5

If this concept is not familiar to you, please view our post on absolute value equations before continuing with this example.

Be sure to consider both values!

To solve an absolute value inequality in the form |ax + b| > c, you need to solve for the following two inequalities:

ax + b > c

ax + b < –c

Now let’s look at an example.

Example:  Solve for x in | 2x – 6| > 8

Answers:  x > 7  and  x < –1

STEP 1: 

Solve for the value of c in the form ax + b > c .

2x – 6 > 8

2x – 6 + 6 > 8 + 6

2x  > 8 + 6

2x > 14

2x ÷ 2 > 14 ÷ 2

x > 7

STEP 2:  

Solve for the value of –c in the form ax + b < –c .

2x – 6 <  –8

2x – 6 + 6 <  –8 + 6

2x  <  –8 + 6

2x  <  –2

2x ÷ 2 <  –2 ÷ 2

x < –1

Absolute Inequality Rule

Be careful not to confuse solving absolute value inequalities with the absolute value inequality rule.

The absolute value inequality rule says that the absolute value of the sum of two numbers is always less than or equal to the sum of the absolute values of the individual numbers.

Using the absolute value symbols |  | , we can represent this rule as follows:

| x + y |  ≤  |x| + |y|

Absolute Inequality Proof

We can prove that this rule is true, when a = 2 and b = –3, for example:

| x + y |  ≤  |x| + |y|

| 2 + –3 |  ≤  |2| + |–3|

| 2 – 3 |  ≤  2 + 3

| –1 |  ≤  2 + 3

1  ≤  2 + 3

1  ≤  5

Solving Inequalities – Quadratic Inequality Example

You will remember from our post on quadratic forms that a quadratic has a variable that is raised to the power of two.

When working with quadratics, you need to bear in mind that there will usually be more than one possible solution to a quadratic inequality.

Let’s look at an example of how to solve a quadratic inequality.

Example:   Solve for possible values of x.

x² + 2x > 15

Answers:   x < –5  and  x > 3

STEP 1:  

Move the terms to one side of the inequality so that you have just zero on one side.

x² + 2x > 15

x² + 2x – 15 > 15 – 15

x² + 2x – 15 > 0

STEP 2:  

Factor the quadratic. If you do not know how to to this, please see our post on factoring quadratics before you finish studying this example.

x² + 2x – 15 > 0

(x – 3)(x + 5) > 0

STEP 3:  

Find possible values for x by making the value inside each set of parentheses equal to zero.

For the first set of parentheses (x – 3),  we would need to replace x with 3 to make the value zero (because 3 – 3 = 0).

So, we know for this set of parentheses that x > 3.

For the second set of parentheses (x + 5),  we would need to replace x with –5 to make the value zero (because –5 + 5 = 0).

To solve this part of the quadratic, we need to reverse the way the sign points.

So, we know for the second set of parentheses that x < –5.

STEP 4:  

Check for possible values of x.

From step 3 above, we know that x > 3.

So, replace x for a value that is greater than 3.

We will use 4 as an example in our proof for this quadratic.

(x – 3)(x + 5) > 0

(4 – 3)(4 + 5) > 0

(4 – 3)(4 + 5) > 0

1 × 9 > 0

9 > 0

Check Your Answer

Now check your other possible answer.

From step 3 above, we also know that x < –5.

So, replace x with a value that is less than –5.

We will use –6 as an example in our proof for the quadratic.

(x – 3)(x + 5) > 0

(–6 – 3)(–6 + 5) > 0

(–6 – 3)(–6 + 5) > 0

–9  × –1 > 0

9 > 0

So, our answers are  x < –5 and x > 3.

Solve Multi Step Inequalities – Practical Problems

You may also need to know how to use inequalities to solve practical problems like the one in this section

Example:   In the equations below, x represents the cost of a pair of jeans and y represents the cost of a pair of shoes. If we know that x – 3 > 5 and y = x – 3, then the cost of 2 pairs of shoes is greater than which one of the following?

A.   x − 2

B.   x − 5

C.   y + 5

D.   5

E.    10

Look for Common Terms

For problems like this, look to see if both of the equations have any variables or terms in common.

In this problem, both equations contain x − 3.

The cost of one pair of shoes is represented by y, and y is equal to x − 3.

Therefore, we can substitute values from one equation to another.

x − 3 > 5

y > 5

If two pairs of jeans are being purchased, we need to solve for 2y.

y × 2 > 5 × 2

2y > 10

So, the correct answer is E.

Further Exercises

You may also want to view our posts on:

Number lines

Interval notation

For help with rational inequalities, please see our posts on algebraic fractions.

For more help with graphing inequalities, please see our posts on graphing.

How to Solve Simultaneous Equations – Quiz

In this post, we look at how to solve simultaneous equations problems on your algebra test.

Instructions: Use the elimination method to solve systems of equations questions 1 to 3.  Use the substitution method to solve systems of equations questions 4 and 5.

[WpProQuiz 32]

Solve Simultaneous Equations – Linear Equations

For simultaneous equations problems, you will see two equations that have common variables, such as x or y.

You will see systems of equations questions where both of the equations are linear equations.

Elimination Method Example

Look the example below, in which both equations are linear.

Example:  Solve for a and b if a + b = 3 and 3a – b = 17.

Answer:  a = 5 and b = –2

We will use the elimination method in the solution that follows.

STEP 1:  Make one equation

Make one equation from the two equations as shown.

You make one equation by combining the left sides of the two equations together, then placing the equals sign in the new equation, and then combining the right sides together.

a + b = 3 and 3a – b = 17  →

a + b + 3a – b = 3 + 17

STEP 2:  Group like terms together

Group like terms together and simplify.

a + b + 3a – b = 3 + 17

a + 3a + b – b = 3 + 17

a + 3a – b + b = 3 + 17

a + 3a = 3 + 17

4a = 20

STEP 3:  Divide to solve

Perform division to solve for a.

4a = 20

4a ÷ 4 = 20 ÷ 4

a = 5

STEP 4:  Replace variable with its value

Replace variable “a” with its value in one of the equations.

a = 5  and  a + b = 3  so,

a + b = 3   →  5 + b = 3

STEP 5:  Solve for the other variable

Solve for the other variable, which is “b” in this problem.

5 + b = 3

5 – 5 + b = 3 – 5

5 – 5 + b = 3 – 5

b = 3 – 5

b = –2

The example above assumes that your systems of equations have like terms.

If this is not the case, you will need to perform multiplication in order to create like terms before you carry out the elimination method.

Click on the following link for help with advanced problems on the elimination method.

Solve Systems of Equations – Linear & Quadratic Equations

In the example below, one equation is linear and the other is quadratic.

Example:  Solve for x and y if x² + y² = 9 and y – 3x = 1

STEP 1:  Isolate variable y in the linear equation

In order to solve systems of equations in this type of question, you need to isolate y in the linear equation:

y – 3x = 1

y – 3x + 3x = 1 + 3x

y – 3x + 3x = 1 + 3x

y = 1 + 3x

STEP 2:  Substitute 1 + 3x for y

In the quadratic equation, you need to substitute 1 + 3x for y.

x² + y² = 9 is our quadratic equation.

x² + y² = 9

(1 + 3x)² + y² = 9

STEP 3:  FOIL Method and Quadratic Formula

You then need to use the FOIL method and the quadratic formula to solve systems of equations problems that include quadratic equations.

Please see our exercises on the FOIL method and the quadratic formula for further exercises on these skills.

You can also solve systems of equations problems graphically.

We will cover this skill in our posts on graphing.

More Exam Preparation

If you are taking a math placement test, you may also want to view the following:

How to Factor in Algebra Problems

Help with Quadratic Equations

Get the downloads

Rational Numbers That Are Not Integers – Fractions, Decimals, Ratios

Rational numbers that are not integers can be written as fractions, ratios, terminating decimals, or repeating decimals.

Rational Numbers – Exercises

Instructions:  For questions 1 to 5, identify the rational numbers from the lists provided. For questions 6 to 8, express the rational numbers in their simplest form. For questions 9 and 10, rationalize the denominator. You may want to study the examples below first.

1)   3.456382 , 176739/892548 , 4p

2)   582 , 1/3 , \(\frac{2}{\sqrt{4}}\)

3)  9: 1 , 0.5876 , \(\sqrt{3}\)

4)   1/6 , 1589572 , \(\sqrt{2}\)

5)    24/72, \(\frac{\pi}{\sqrt{16}}\) ,   \(\frac{\sqrt{3} – 1}{-2}\)

6)   \(\frac{1}{3} \times \frac{3}{5}\)

7)   \(\frac{1}{6} \div \frac{4}{9}\)

8)   \(\frac{x/y}{v/w}\)

9)   \(\frac{3}{\sqrt{2}}\)

10)   \(\frac{5}{\sqrt{3}}\)

Rational Numbers – Answers

Answer to question 1

1)   The correct answers are:

3.456382  and  176739/892548

3.456382 is rational because it is a terminating decimal.

176739/892548 is rational because it is a fraction. When simplified, it is also a terminating decimal.

4p is not rational because it is a non-terminating decimal.

Answer to question 2

2)   The correct answers are:

582 , 1/3 , and  \(\frac{2}{\sqrt{4}}\)

582 is rational because it is an integer.

1/3 is rational because it is a repeating decimal.

\(\frac{2}{\sqrt{4}}\) is rational because it can be simplified to 1.

Answer to question 3

3)  The correct answers are:

9: 1  and 0.5876

9: 1 is rational because it is a ratio.

0.5876 is rational because it is a repeating decimal.

\(\sqrt{3}\) is not rational because it is a non-terminating decimal.

Answer to question 4

4)   The correct answers are:

1/6  and 1589572

1/6 is rational because it is a fraction. When simplified, it is also a repeating decimal.

1589572 is rational because it is an integer.

\(\sqrt{2}\) is not rational because it is a non-terminating decimal.

Answer to question 5

5)    The correct answers is:  24/72

24/72 is rational because is a fraction. When simplified, it is also a repeating decimal.

\(\frac{\pi}{\sqrt{16}}\) is not rational because p is a non-terminating decimal.

\(\frac{\sqrt{3} – 1}{-2}\) is not rational, even through the denominator has been rationalized. That is because the square root of 3 is a non-terminating decimal.

Answer to question 6

6)   The correct answer is:  1/5

When you multiply fractions, you have to multiply the numerators and then the denominators. Then simplify, if possible.

\(\frac{1}{3} \times \frac{3}{5} =\)

\(\frac{1 \times 3}{5 \times 3} =\)

\(\frac{3}{15} =\)

\(\frac{1}{5}\)

Answer to question 7

7)   The correct answer is:  3/8

When you divide fractions, you have to invert the second fraction and then multiply.

\(\frac{1}{6} \div \frac{4}{9} =\)

\(\frac{1}{6} \times \frac{9}{4} =\)

\(\frac{1 \times 9}{6 \times 4} =\)

\(\frac{9}{24} =\)

\(\frac{3 \times 3}{3 \times 8} =\)

\(\frac{3}{8} \)

Answer to question 8

8)   The correct answer is:  xw/yv

When you divide fractions that are rational expression like this one, you have to invert the second fraction and then multiply.

\(\frac{x/y}{v/w} =\)

\(\frac{x}{y} \div \frac{v}{w} =\)

\(\frac{x}{y} \times \frac{w}{v} =\)

\(\frac{x \times w}{y \times v} =\)

\(\frac{xw}{yv}\)

Answer to question 9

9)   The correct answer is:

\(\frac{3\sqrt{2}}{2}\)

Multiply both the numerator and the denominator by the square root in order to rationalize the denominator.

\(\frac{3}{\sqrt{2}} = \)

\(\frac{3 \times \sqrt{2}}{\sqrt{2}\times \sqrt{2}} = \)

\(\frac{3\sqrt{2}}{2}\)

Answer to question 10

10)   The correct answer is:

\(\frac{5\sqrt{3}}{3}\)

Multiply both the numerator and the denominator by the square root in order to rationalize the denominator.

\(\frac{5}{\sqrt{3}}\)

\(\frac{5 \times \sqrt{3}}{\sqrt{3}\times \sqrt{3}} = \)

\(\frac{5\sqrt{3}}{3}\)

Simplifying Rational Numbers

You will need to simplify rational number integers, as well as rational numbers that are not integers, on your algebra exam.

Expressing fractions in their simplest form may involve adding, subtracting, multiplying, or dividing fractions, as well as finding the lowest common denominator.

You may want to view our pages on fractions and decimals if you need to review these skills.

Now look at the following example question.

Simplifying Rational Numbers – Example 1

Identify the rational numbers in the following list.

3 , 1/4 , 0.256733 ,  π , 1: 5 , \(\sqrt{2}\)

Answer:   3 , 1/4 , 0.256733 ,  1: 5

• 3 is a rational number because it is an integer.
• 1/4 is a rational number because it is a fraction.
• 0.256733   is a rational number because it is a repeating decimal.
•  π is not a rational number because it is a non-terminating decimal.
• 1: 5 is a rational number because it is a ratio. It can also be expressed as a fraction.
• \(\sqrt{2}\) is not a rational number because it is a non-terminating decimal, when simplified.

What is a Rational Number – with Example

Rational numbers can be expressed in the form a/b where a and b are integers and b is not zero.

Rational Numbers – Integers

Integers are rational numbers because they can be written in the form a/b.

For example, the integer 7 can be written as 7/1.

So, integers are rational numbers because they can be written as fractions, with the integer in the numerator and 1 in the denominator.

Rational Numbers That Are Not Integers – Denominators

You may see questions on your algebra test that ask you to rationalize the denominator in a fraction.

This means that you have to express the denominator as a rational number.

The denominator may include a radical or polynomial.

So, you may need to know how to carry out the FOIL method in order to rationalize a denominator.

Look at the following example.

Example 2:  

Rationalize the denominator in the fraction below.

\(\frac{1}{1 + \sqrt{3}}\)

Answer: 

\(\frac{1 – \sqrt{3}}{-2}\)

Now study the steps in the solution below

Use the FOIL method to simplify the denominator.

\(\frac{1}{1 + \sqrt{3}} =\)

\(\frac{1}{1 + \sqrt{3}} \times \frac{1 – \sqrt{3}}{1 – \sqrt{3}} =\)

\(\frac{1 \times (1 – \sqrt{3})}{(1 + \sqrt{3})(1 – \sqrt{3})}  =\)

\(\frac{1 – \sqrt{3}}{1^2 + \sqrt{3} – \sqrt{3} – \sqrt{3}^2} \)

Then perform the subtraction and simplify the square root to simplify further.

\(\frac{1 – \sqrt{3}}{1^2 + \sqrt{3} – \sqrt{3} – \sqrt{3}^2}  =\)

\(\frac{1 – \sqrt{3}}{1 – 3} =\)

\(\frac{1 – \sqrt{3}}{-2}\)

More Algebra Practice

Numbers that are not rational numbers are called irrational numbers.

You may want to see our posts on irrational numbers and radicals.

Get the math download

Simplifying Algebraic Expressions – Examples & Exercises

You may want to study the “simplifying algebraic expressions examples” in the next section before attempting the quiz below.

Simplifying Expressions – Exercises

Instructions:  Simplify the expressions that follow. Then check your answers in the next section.

1)   10x + 5y – 6x  + 12 + 3y – 6

2)   12a – 15 + 3c – 14 + 14b – 6a + 10 – 8c – 20b

3)   5x(3x²y + 2)

4)   \(\text 3 \times \frac{\sqrt{2}}{3}\)

5)   \(\frac{a^2 + ab}{a}\)

Simplifying Expressions – Answers

Answer to question 1

1)   The correct answer is:  4x + 8y + 6

10x + 5y – 6x  + 12 + 3y – 6 =
10x – 6x + 5y – 6x  + 12 + 3y – 6 =
10x – 6x + 5y + 12 + 3y – 6 =
4x + 5y + 12 + 3y – 6 =
4x + 5y + 3y + 12 + 3y – 6 =
4x + 5y + 3y + 12 – 6 =
4x + 8y + 12 – 6 =
4x + 8y + 6

Answer to question 2

2)   The correct answer is:  6a – 6b – 5c – 19

12a – 15 + 3c – 14 + 14b – 6a + 10 – 8c – 20b =
12a – 6a – 15 + 3c – 14 + 14b – 6a + 10 – 8c – 20b =
12a – 6a – 15 + 3c – 14 + 14b + 10 – 8c – 20b =
6a – 15 + 3c – 14 + 14b + 10 – 8c – 20b =
6a + 14b – 15 + 3c – 14 + 14b  + 10 – 8c – 20b =
6a + 14b – 15 + 3c – 14 + 10 – 8c – 20b =
6a + 14b – 20b – 15 + 3c – 14 + 10 – 8c – 20b =
6a + 14b – 20b – 15 + 3c – 14 + 10 – 8c =
6a – 6b – 15 + 3c – 14 + 10 – 8c =
6a – 6b + 3c – 15 + 3c – 14 + 10 – 8c =
6a – 6b + 3c – 15 – 14 + 10 – 8c =
6a – 6b + 3c – 8c – 15 – 14 + 10 – 8c =
6a – 6b + 3c – 8c – 15 – 14 + 10 =
6a – 6b – 5c – 15 – 14 + 10 =
6a – 6b – 5c + (–15 – 14 + 10) =
6a – 6b – 5c – 19

Answer to question 3

3)   The correct answer is:  15x³y + 10x

5x(3x²y + 2) =
(5x × 3x²y) + (5x × 2) =
15x³y + (5x × 2) =
15x³y + 10x

Answer to question 4

4)   The correct answer is:  \(\sqrt{2}\)

\(\text 3 \times \frac{\sqrt{2}}{3} =\)
\(\frac{3 \times \sqrt{2}}{3} =\)
\(\sqrt{2}\)

Answer to question 5

5)   The correct answer is:  a + b

\(\frac{a^2 + ab}{a} =\)
\(\frac{a(a + b)}{a} =\)
\(\frac{a \times (a + b)}{a} =\)
\(\text a + b\)

Simplifying Algebraic Expressions – Examples and Explanations

In order to learn the process of simplifying algebraic expressions, you need examples showing you how to combine like terms.

When you combine like terms on “simplifying expressions” problems on your algebra test, you usually have to add or subtract.

Look at the example that follows.

Example:  Simplify 5x + 3y – 2x  + 10 + 2y – 4

Answer:  3x + 5y  + 6

Step 1:  Simplify for one of the algebraic terms

First of all, we will rearrange the expression to put the x terms together.

5x + 3y – 2x  + 10 + 2y – 4 =

5x – 2x + 3y – 2x  + 10 + 2y – 4 =

5x – 2x + 3y  + 10 + 2y – 4

Then perform the subtraction on the x term:

5x – 2x   3y  + 10 + 2y – 4 =

3x + 3y + 10 + 2y – 4

Step 2:  Simplify for the other algebraic terms

Next, we need to rearrange the expression to put the y terms together.

3x + 3y + 10 + 2y – 4 =

3x + 3y + 2y + 10 + 2y – 4 =

3x + 3y + 2y + 10 – 4

Then perform the addition on the y term:

3x + 3y + 2y + 10 – 4 =

3x + 5y + 10 – 4

Step 3:  Simplify for the constants

You will remember from our post on algebraic terms, that constants are the terms in an expression that do not have variables.

So, in our expression 3x + 5y + 10 – 4, the integers 10 and –4 are the constants.

Finally, we need to perform the subtraction on the constants.

3x + 5y + 10 – 4 =

3x + 5y + 6

Step 4: Check your result

Check to see if any further simplification is possible.

In our previous step, we had the result of 3x + 5y + 6.

We can see from the expression above that there is only one x term, only one y term, and only one constant.

So, we have simplified the expression as much as possible.

Visit Us on YouTube

Simplifying Expressions on Your Exam

You will have several problems on simplifying expressions on your algebra test.

What is "Simplifying Algebraic Expressions"?

The phrase "simplifying expressions" means that you need to put an algebraic expression in its simplest form.

So, in order to simplify, you need to perform any mathematical operations that you can in the expression.

You may need to add, subtract, multiply, divide, simplify fractions, or deal with exponents or square roots when you are simplifying expressions.

If you have not already done so, you may want to have a look at our post on Order of Operations (PEMDAS) before you continue reading this post.

If you feel that need further practice with simplifying expressions, please see the following posts before you try the exercises in the next section:

Grouping Like Terms

Simplification - Advanced Problems

Further Exam Practice

You may also want to see our posts on:

Exponent Laws

Quadratic Expressions

Factoring Expressions

The Square Root on Your Algebra Exam

There will be several questions on the square root on your algebra test.

Square roots are written with the radical symbol.

SQUARE ROOT EXERCISES

Instructions:  Solve the problems that follow without using the square root calculator.

1)   \(\sqrt{196} = \text ?\)

2)   \(\sqrt{121} = \text ?\)

3)   \(\sqrt{225} = \text ?\)

4)   Express as a decimal number:

\(\sqrt{400} + \frac{10}{\sqrt{400}}= \text ?\)

5)   \(\sqrt{3.24} = \text ?\)

6)   \(\sqrt{82}\) lies between which set of integers?

A.  6 and 7

B.  7 and 8

C.  8 and 9

D.  9 and 10

7)   \(\sqrt{35}\) lies between which set of integers?

A.  4 and 5

B.  5 and 6

C.  6 and 7

D.  7 and 8

8)   Approximate \(\sqrt{164}\) to one decimal place.

9)   \(– \sqrt{25} = \text ?\)

10)   \(\sqrt{-5} = \text ?\)

Square Roots – Answers

Answer to question 1

1)   The correct answer is:  14

196 is a perfect square:

\(\sqrt{196} = 14\)

Answer to question 2

2)   The correct answer is:  11

121 is a perfect square:

\(\sqrt{121} = 11\)

Answer to question 3

3)   The correct answer is:  15

225 is another perfect square:

\(\sqrt{225} = 15\)

Answer to question 4

4)   The correct answer is:  20.5

We need to express our result as a decimal number.

First of all, find the square root.

\(\sqrt{400} = 20\)

Then, substitute the values.

\(\sqrt{400} + \frac{10}{\sqrt{400}}= \)

\(\text 20 + \frac{10}{20}= \)

\(\text 20 + \frac{1}{2}\)

Finally, express the fraction as a decimal to solve.

\(\text 20 + \frac{1}{2} = 20.5\)

Answer to question 5

5)   The correct answer is:  1.8

We know that \(\sqrt{324} = 18\).

So, move the decimal place to solve.

\(\sqrt{3.24} = 1.8\)

Answer to question 6

6)   The correct answer is:  D

\(\sqrt{81} = 9\) and \(\sqrt{100} = 10\)

82 lies between 81 and 100.

So, \(\sqrt{82}\) lies between 9 and 10.

Answer to question 7

7)   The correct answer is:  B

\(\sqrt{25} = 5\) and \(\sqrt{36} = 6\)

35 lies between 25 and 36.

So, \(\sqrt{35}\) lies between 5 and 6.

Answer to question 8

8)   The correct answer is:  12.8

We have to approximate \(\sqrt{164}\) to one decimal place.

For the approximation method, remember the square roots from the chart and think of the nearest ones.

The square root of 169 is 13, so the square root of 164 will be very close to the square root of 169.

Try from 12.9 and work downwards.

12.9 × 12.9 = 166.4

12.8 × 12.8 = 163.8

12.7 × 12.7 = 161.3

163.8 is the closest to 164, so the answer is 12.8.

Answer to question 9

9)   The correct answer is:   –5

The negative sign is outside the square root symbol.

So, first of all find \(\sqrt{25}\).

We know from our chart that \(\sqrt{25} = 5\)

To solve, we add the negative sign:  –5

Answer to question 10

10)   The correct answer is:  an imaginary number

We cannot multiply any real number by itself to get a negative number.

So, \(\sqrt{-5} = i\)

Square and Square Roots

To square a number, we multiply that number by itself.

A number squared uses the exponent 2.

So, a square looks like this: 4²

A square root is a number that we multiply by itself to get the result specified inside the square root symbol.

The square root symbol is:  \(\sqrt{16}\)

When we multiply 4 by itself, we get 16.

So, 4 is the square root of 16.

Mathematically, this is represented as:

\(\sqrt{16} = 4\)

Square Roots – Chart

You should study the square roots in the chart below before you take your exam.

After you have learned the following square roots by heart, try the practice exercises in the second-to-last section of this post.

Estimating Square Roots

The square roots in the chart in the previous section are known as square roots of perfect squares.

In other words, the square roots of the numbers in the chart above are whole numbers.

You might need to use the “approximation method” for square roots that are not whole numbers.

For the approximation method, remember the square roots from the chart above and then try to think of the nearest one.

Look at the example below.

Example:  Estimate to one decimal place \(\sqrt{24}\)

Answer:  4.9

We know that the square root of 25 is 5, so the square root of 24 will be very close to the square root of 25.

Try from 4.9 and work downwards.

4.9 × 4.9 = 24.01

4.8 × 4.8 = 23.04

24.01 is closer to 24 than 23.04.

So, 4.9 is the correct answer.

Square Root Calculator

On your exam, you will need to know most of the square roots for perfect squares by heart.

So, we suggest memorizing the square roots in the chart in the section above.

If you need to find square roots for a decimal number or for advanced problems on square roots, you may want to use the square root calculator.

To use the calculator, please click on the link below.

Square Root Calculator

 Further Algebra Practice

For further algebra practice,  see our posts on decimals, fractions, and exponents.

You may also want to see our posts on radicals and imaginary numbers.

Quadratic Formula – Steps to Solve Problems

Use the quadratic formula steps below to solve problems on quadratic equations.

For the free practice problems, please go to the third section of the page.

Using the Quadratic Formula – Steps

Quadratic equations are in this format:  ax² ± bx ± c = 0

Look at the following example of a quadratic equation:

x² – 4x – 8 = 0

Use the quadratic formula steps below to solve.

Step 1: Coefficients and constants

First of all, identify the coefficients and constants.

“Coefficients” are the a and b variables in the equation. c is a constant.

Our equation is:  x² – 4x – 8 = 0

In our equation a = 1.  1 is the coefficient because: x² × 1 = x²

The second term of our equation is – 4x, so b = –4.

Finally, the third term of our equation is – 8, so c = –8.

Step 2: Substitute value for b

Substitute the value for b and perform the operations.

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{–4 \pm \sqrt{-4^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{4 \pm \sqrt{16 – 4ac}}{2a}\)

Step 3: Substitute values for a and c

Substitute the values and perform the operations to solve for x.

Remember that a = 1 and c = –8.

\(\text{x} = \frac{4 \pm \sqrt{16 – 4ac}}{2a}\)

\(\text{x} = \frac{4 \pm \sqrt{16 – (4 \times 1 \times -8)}}{2 \times 1}\)

\(\text{x} = \frac{4 \pm \sqrt{16 + 32}}{2}\)

\(\text{x} = \frac{4 \pm \sqrt{48}}{2}\)

Quadratic Formula – Exercises

Instructions:  Solve each quadratic equation for x using the quadratic formula.  If your answer is not a positive or negative integer, you may leave it as an unsimplified fraction as in the examples above.

1)   x² + 13x +36 = 0

2)   x² + 3x – 10 = 0

3)   2x² – 20x + 32 = 0

4)   3x² – 6x – 45 = 0

5)   4x² – 2x – 41 = 0

Quadratic Formula – Answers

1)   The answers are: –9 and –4

x² + 13x + 36 = 0

a = 1     b = 13     c = 36

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{-13 \pm \sqrt{13^{2} – (4 \times 1 \times 36)}}{2 \times 1}\)

\(\text{x} = \frac{-13 \pm \sqrt{169 – 144}}{2}\)

\(\text{x} = \frac{-13 \pm \sqrt{25}}{2}\)

\(\text{x} = \frac{-13 \pm 5}{2}\)

\(\text{x} = \frac{-13 – 5}{2} = \frac{-18}{2} = -9 \)

\(\text{x} = \frac{-13 + 5}{2} = \frac{-8}{2} = -4 \)

2)   The answers are: –5 and 2

x² + 3x – 10 = 0

a = 1     b = 3     c = –10

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{-3 \pm \sqrt{3^{2} – (4 \times 1 \times -10)}}{2 \times 1}\)

\(\text{x} = \frac{-3 \pm \sqrt{9 +40}}{2}\)

\(\text{x} = \frac{-3 \pm \sqrt{49}}{2}\)

\(\text{x} = \frac{-3 \pm 7}{2}\)

\(\text{x} = \frac{-3 – 7}{2} = \frac{-10}{2} = -5 \)

\(\text{x} = \frac{-3 + 7}{2} = \frac{4}{2} = 2 \)

3)   The answers are:  2 and 8

2x² – 20x + 32 = 0

a = 2     b = –20     c = 32

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{–20 \pm \sqrt{-20^{2} – (4 \times 2 \times 32)}}{2 \times 2}\)

\(\text{x} = \frac{20 \pm \sqrt{400 – 256}}{4}\)

\(\text{x} = \frac{20 \pm \sqrt{144}}{4}\)

\(\text{x} = \frac{20 \pm 12}{4}\)

\(\text{x} = \frac{20 – 12}{4} = \frac{8}{4} = 2 \)

\(\text{x} = \frac{20 + 12}{4} = \frac{32}{4} = 8 \)

4)   The answers are: –3 and 5

3x² – 6x – 45 = 0

a = 3     b = –6     c = –45

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{–6 \pm \sqrt{-6^{2} – (4 \times 3 \times -45)}}{2 \times 3}\)

\(\text{x} = \frac{6 \pm \sqrt{36 + 540}}{6}\)

\(\text{x} = \frac{6 \pm \sqrt{576}}{6}\)

\(\text{x} = \frac{6 \pm 24}{6}\)

\(\text{x} = \frac{6 – 24}{6} = \frac{-18}{6} = -3 \)

\(\text{x} = \frac{6 + 24}{6} = \frac{30}{6} = 5 \)

5)   The answers is:  \(\text{x} = \frac{2 \pm 14\sqrt{47}}{8}\)

4x² – 2x – 41 = 0

a = 4     b = –2     c = –41

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{–2 \pm \sqrt{-2^{2} – (4 \times 4 \times -41)}}{2 \times 4}\)

\(\text{x} = \frac{2 \pm \sqrt{2 + 256}}{8}\)

\(\text{x} = \frac{2 \pm \sqrt{658}}{8}\)

\(\text{x} = \frac{2 \pm 14\sqrt{47}}{8}\)

Format of the Quadratic Formula

You will need to use the quadratic formula on several algebra problems on your math test.

The quadratic formula is in this format:

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

Although the quadratic formula may look confusing and difficult, using it is really quite simple.

All you have to do is identify a, b, and c, and then put in the values from the equation provided.

Then you can solve for x.

Sample Exercise

Use the quadratic formula to solve for x in the following problem:

5x² + x – 3 = 0

Work out your answer on a piece of paper.

Then check your answer against the solution below.

Answer to the Exercise

Step 1:

Write down the coefficients and constant.

Remember that the basic format of the equation is:

ax² ± bx ± c = 0

And our equation is:  5x² + x – 3 = 0

So, in our equation a = 5.

The second term of our equation is x, so b = 1.

Finally, the third term of our equation is – 3, so c = –3.

Step 2:

Substitute the value for b in the quadratic formula and perform the operations.

\(\text{x} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{-1 \pm \sqrt{1^{2} – 4ac}}{2a}\)

\(\text{x} = \frac{-1 \pm \sqrt{1 – 4ac}}{2a}\)

Step 3:

Substitute the values for a and c in the quadratic formula and

perform the operations in order to solve.

Remember that a = 5 and c = –3.

\(\text{x} = \frac{-1 \pm \sqrt{1 – 4ac}}{2a}\)

\(\text{x} = \frac{-1 \pm \sqrt{1 – (4 \times 5 \times -3)}}{2 \times 5}\)

\(\text{x} = \frac{-1 \pm \sqrt{1 + 60}}{10}\)

\(\text{x} = \frac{-1 \pm \sqrt{61}}{10}\)

We look at the quadratic equation in more depth in another post.

You may also want to view the following posts:

FOIL method

Quadratic Expressions

Solving Factored Quadratic Equations

More Free Algebra Practice

Simplifying Radical Expressions – Examples Page

You will need to understand the process of simplifying radical expressions and study some examples for your algebra exam.

In particular, you will need to know how to factor radicals, how to perform operations such as addition and multiplication on radicals, and how to express radicals as rational numbers.

Simplifying Radical Expressions – Exercises

1)    Factor: \(\sqrt{98}\)

2)    Simplify: \(\sqrt{20} + 2\sqrt{45} + 4\sqrt{180}\)

3)    Simplify: \(\sqrt{28} + 5\sqrt{63} + 4\sqrt{112}\)

4)   Simplify: \(\sqrt{7} \times \sqrt{13}\)

5)   \(\sqrt[3]{\frac{216}{343}} = ?\)

Radicals – Answers

1)    The correct answer is:  \(7\sqrt{2}\)

\(\sqrt{98} = \sqrt{49 \times 2} = \sqrt{49} \times \sqrt{2} =7\sqrt{2}\)

2)    The correct answer is:  \(32\sqrt{5}\)

\(\sqrt{20} + 2\sqrt{45} + 4\sqrt{180} =\)

\(\sqrt{4 \times 5} + (2\sqrt{9 \times 5}) + (4\sqrt{36 \times 5}) =\)

\(2\sqrt{5} + (2 \times 3\sqrt{5}) + (4 \times 6\sqrt{5}) =\)

\(2\sqrt{5} + 6\sqrt{5} + 24\sqrt{5} =\)

\(32\sqrt{5}\)

3)    The correct answer is:  \(33\sqrt{7}\)

\(\sqrt{28} + 5\sqrt{63} + 4\sqrt{112} =\)

\(\sqrt{4 \times 7} + (5\sqrt{9 \times 7}) + (4\sqrt{16 \times 7}) =\)

\(2\sqrt{7} + (5 \times 3\sqrt{7}) + (4 \times 4\sqrt{7}) =\)

\(2\sqrt{7} + 15\sqrt{7} + 16\sqrt{7} =\)

\(33\sqrt{7}\)

4)   The correct answer is:  \(\sqrt{91}\)

\(\sqrt{7} \times \sqrt{13} =\)

\(\sqrt{7 \times 13} =\)

\(\sqrt{91}\)

5)   The correct answer is:  \(\frac{6}{7}\)

\(\sqrt[3]{\frac{216}{343}} = \)

\(\sqrt[3]{\frac{6 \times 6 \times 6}{7 \times 7 \times 7}} = \)

\(\frac{6}{7}\)

Factoring Radicals

When you simplify radical expressions, you need to find the factors of each of the radicals in the expression first.

Simplifying Radical Expressions Examples – 1 

Which of the answers below is equal to \(\sqrt{192}?\)

A.  1 ÷ 192
B.  \(\text 3\sqrt{64}\)
C.  \(\text 64\sqrt{3}\)
D.  \(\text 8\sqrt{3}\)
E.  \(\text 3\sqrt{8}\)

Answer:  The correct answer is D

For radical problems like this one, you need to remember certain mathematical principles.

To start with, remember to factor the number inside the radical sign.

The factors of 192 are:

1 × 192 = 192
2 × 96 = 192
3 × 64 = 192
4 × 48 = 192
6 × 32 = 192
8 × 24 = 192

Then look to see if any of these factors are perfect squares.

In this case, the largest factor that is a perfect square is 64.

Now find the square root of 64.

\(\sqrt{64} = 8\)

Finally, you need to put this number at the front of the radical sign and put the other factor inside the radical sign in order to solve the problem.

\(\sqrt{192} = \sqrt{64} \times \sqrt{3} =\text 8\sqrt{3}\)

Simplifying Radical Expressions – Advanced Examples

Your exam may have advanced problems on simplifying radical expressions involving other operations, such as addition or subtraction.

Example 2:  

\(\sqrt{32} + 2\sqrt{50} + 3\sqrt{18} = ?\)

A.  \(5\sqrt{100}\)
B.  \(6\sqrt{100}\)
C.  \(30\sqrt{4}\)
D.  \(2\sqrt{23}\)
E.  \(23\sqrt{2}\)

Answer:  

The correct answer is E

The first step is to find the factors of the amounts inside the radical signs.

Then look to see if any of these factors are perfect squares.

\(\sqrt{32}  = \sqrt{16} \times \sqrt{2}\)

\(\text2\sqrt{50} = \text 2 \times \sqrt{25} \times \sqrt{2}\)

\(\text3\sqrt{18} = \text 3 \times \sqrt{9} \times \sqrt{2}\)

Then simplify the factors that are perfect squares and add up.

\(\sqrt{32} + 2\sqrt{50} + 3\sqrt{18} = \)

\((\sqrt{16} \times \sqrt{2}) + (\text 2 \times \sqrt{25} \times \sqrt{2}) + (\text 3 \times \sqrt{9} \times \sqrt{2}) = \)

\((4 \times \sqrt{2}) + (\text 2 \times 5 \times \sqrt{2}) + (\text 3 \times 3 \times \sqrt{2}) = \)

\((4\sqrt{2}) + (10\sqrt{2}) + (9\sqrt{2}) = \)

\((4 + 10 + 9) \times \sqrt{2} = 23\sqrt{2}\)

Multiplication of Radicals

Simplifying Radical Expressions Example 3:  

\(\sqrt{3} \times \sqrt{5} = ?\)

A.  \(\sqrt{15}\)
B.  \(\sqrt{8}\)
C.  \(3\sqrt{5}\)
D.  \(5\sqrt{3}\)
E.  \(\sqrt{-1}\)

Answer:  The correct answer is A

Multiply the numbers inside the radical signs.

Then put this result inside a radical symbol for your answer.

\(\sqrt{3} \times \sqrt{5} = \sqrt{3 \times 5} = \sqrt{15}\)

Rationalizing Radicals

You may see problems on the exam that ask you to rationalize a number or to express a radical number as a rational number.

Simplifying Radical Expressions – Examples 4

Express the following as a rational number:

\(\sqrt[3]{\frac{64}{125}} = ?\)

A.  \(\frac{1}{5}\)

B.  \(\frac{4}{5}\)

C.  \(\frac{5}{4}\)

D.  \(\frac{64}{125}\)

E.  \(\frac{125}{64}\)

Answer:  

The correct answer is B

In this problem, you have to find the cube roots of the numerator and denominator in order to eliminate the radical.

\(\sqrt[3]{\frac{62}{125}} = \sqrt[3]{\frac{4 \times 4 \times 4}{5 \times 5 \times 5}}= \frac{4}{5}\)

Further Algebra Practice

You may also want to see out posts on:

Perfect Squares

Perfect Cubes

Square Roots

Factoring

Number Line Examples Page

This page has number line examples and exercises for positive and negative number line problems like you will see on your exam.

What are Number Lines?

Number lines can be used to represent inequalities. So, number lines can be drawn from mathematical inequalities. Alternatively, you can determine inequalities from number lines.

When graphing inequalities, you will have to understand positive and negative number line principles.

Positive and Negative Number Line Exercises

1)   Represent the solution to the following on a number line:

3x < –6

2)   Represent the solution to the following on a number line:

–5x – 7 = 3x + 17

3)   Represent the solution to the following on a number line:

–7 <  x  = 2

4)   What inequality is represented on the following number line? 5)   What inequality is represented on the following number line?

Number Lines – Answers

1)   Solve for x first. 3x > –6 3x ÷ 3 > –6 ÷ 3 x  > –6 ÷ 3 x > –2 Then represent the result on a number line. You need to use an open dot because you do not have the equals to sign. We have the “greater than” symbol, so the line needs to point to the right. 2)   Solve for x first. –5x – 7 = 3x + 17 –5x – 7 + 7  = 3x + 17 + 7 –5x  = 3x + 17 + 7 –5x  = 3x + 24 –5x – 3x  = 3x – 3x + 24 –5x – 3x  =  24 –8x  =  24 –8x ÷ –8 =  24 ÷ –8 x  =  24 ÷ –8   We reverse the sign when we divide by a negative. x  =  –3 Then represent the result on a number line. We need to use a solid dot because we have the “less than or equals to” sign. We have the “less than” symbol, so the line needs to point to the left. 3)   Our inequality was:  –7 <  x  = 2 Here we have two values, so the line will not have an arrow on the end of it. One value has the equals to sign, so we need a solid dot for the 2. The other value does not have the equals to sign, so we need an open dot for the –7. The value of x is in the middle, so we need to use a number line to connect the two values as show below. 4)  The answer is:  x = 4 Our number line was: The line points to the left so, we need the less than sign. We also need the equals to sign because the dot is solid. We have the value of 4, so the answer is x = 4. 5)  The answer is: –3 <  x = 5 Our number line was: We have two values, so the line will not have an arrow on the end of it. We have a solid dot for the 5, so this value has the equals to sign. The other value has an open dot, so it does not need the equals to sign. So, the answer is  –3 <  x = 5.

Number Line Examples – 1

In this example, we will look at how to show the solution to an inequality on a number line

The most important thing to remember when working with number lines is the following:

If you multiply or divide by a negative number in an inequality, you must reverse the direction that the inequality sign points.

Now look at the two examples below before you try the practice problems.

Example: Represent the solution to the following on a number line.

25 ≥ –5x

STEP 1:  Begin to solve the inequality by using inverse operations.

We have to divide by a negative number in this example, so we need to reverse the sign from “greater than or equal to” to “less than or equal to.”

25 ≥ –5x

25 ÷ –5 ≥ –5 ÷ –5 x

25 ÷ –5 ≤ x

STEP 2:  Perform the operation to solve.

25 ÷ –5 ≤ x

–5 ≤ x

x ≥ –5

STEP 3:  Set up a number line for the solution.

STEP 4:  Represent the solution on your number line.

For “greater than or equal to” or “less than or equal to” questions, you need to use a solid dot to include the point.

So, we need to place a solid dot on –5.

Then, determine if the line should point to the left (negative) or to the right (positive).

We know that positive numbers are greater than negative numbers, so point the line toward the positive numbers, which are on the right.

As you will see in the next example, if the sign is "greater than" or "less than" (without the "equals to"), you need to use an open circle as the dot to exclude the point.

Number Line Examples - 2

Let's look at an example of how to write inequalities from number lines.

Example:  What inequality is represented on the following number line?

Answer:   x < –3

STEP 1:  Determine the value or values to be used in your inequality.

Our number line begins on –3, so we need to use the value of –3 in our inequality.

STEP 2:  Determine if you should use the "greater than" or "less than" symbol or the "greater than or equal to" or "less than or equal to" symbol.

Here, we have an open dot, so we need to use either the "greater than" or "less than" symbol.

The line is pointing to the left, so we know that we need to use the "less than" symbol.

So, our answer is x < –3.

If the line had been pointing to the right, we would have needed to use the "greater than" symbol.

Further Exercises

You may wish to see our post on inequalities before you attempt the exercises in the previous section.

You can also view our posts on interval notation and graphing.

Solve Each System by Substitution – Quiz

Instructions:  Solve each system by substitution in the quiz that follows. After using the substitution method, check your answers. You may want to view the examples in the next section first.

[WpProQuiz 30]

Solve Each System by Substitution – Step by Step

We can use the substitution method for simultaneous equations. This method helps us solve each system by substitution.

What is the Substitution Method?

We use the substitution method when we substitute numbers for variables in an algebraic expression or formula.

Substitution Method – Example

Study the example below that shows how to use the substitution method in systems of equations.

Example:  Solve for x and y if 3x + 2y = 4 and x + 4y = 3

Answer:  x = 1 and y = 1/2

Step 1:  Label the equations

Label the equations A and B.

(A)  3x + 2y = 4

(B)  x + 4y = 3

Step 2:  Isolate one of the variables

To use the substitution method, we need to isolate one of the variables.

We will isolate variable x in equation B in this example.

x + 4y = 3

x + 4y – 4y = 3 – 4y

x + 4y – 4y = 3 – 4y

x = 3 – 4y

Step 3:  Substitute the value of the isolated variable

Next, you need substitute the value of the variable you have isolated.

We have just determined that x = 3 – 4y.

So, now we substitute 3 – 4y for the value of x in equation A.

Equation A is 3x + 2y = 4.

3x + 2y = 4

3(3 – 4y) + 2y = 4

Step 4:  Perform the multiplication

3(3 – 4y) + 2y = 4

(3 × 3) – (3 × 4y) + 2y = 4

9 – 12y + 2y = 4

Step 5:  Perform inverse operations to solve for y

9 – 12y + 2y = 4

9 – 9 – 12y + 2y = 4 – 9

9 – 9 – 12y + 2y = 4 – 9

–12y + 2y = 4 – 9

–12y + 2y = –5

–10y = –5

–10y ÷ –10 = –5 ÷ –10

y = 1/2

Step 6: Substitute the value of y to solve for x

Finally, we need to substitute the value of y into equation A to solve for x.

We know that equation A is 3x + 2y = 4 and that y = 1/2.

So, substitute the value of y.

3x + 2y = 4

3x + (2 × 1/2) = 4

Then perform the operations to solve for x.

3x + (2 × 1/2) = 4

3x + 1 = 4

3x + 1 – 1 = 4 – 1

3x + 1 – 1 = 4 – 1

3x = 4 – 1

3x = 3

3x ÷ 3 = 3 ÷ 3

x = 1

Substitution Method in Expressions

You will see several questions on your algebra test that ask you to solve an algebraic expression by substituting the value of x or another unknown variable.

Example:   What is the value of  4(3x + 12) when x = 5?

Answer:  108

STEP 1:  Substitute the value of the variable.

4(3x + 12) =

4[(3 × 5) + 12]

STEP 2:  Perform the operations to solve.

4[(3 × 5) + 12] =

4[(15) + 12] =

4(27) =

4 × 27 = 108

Substitution Method in Formulas

You will also see problems on your algebra exam that ask you to use the substitution method in a formula.

In addition, you will need to use the substitution method in this way on the geometry part of the exam.

Example:  The area of a triangle is A = (base × height) ÷ 2. What is the area of a triangle that has a base of 8 units and a height of 6 units?

Answer:  24 units

STEP 1:  Substitute the values into the formula.

A = (base × height) ÷ 2

A = (8 × 6) ÷ 2

STEP 2:  Perform the operations to solve.

A = (8 × 6) ÷ 2

A = 48 ÷ 2

A = 24

Further Algebra Practice

You may also want to view our posts on:

Order of operations

Inverse operations

Grouping like terms

Geometry

Exam SAM on YouTube

Exponents and Powers on Your Exam

You will see several problems involving exponents and powers on your standardized exam.

To see the free sample problems on exponents, please go to the next section.

Exponents and Powers – Exercises

Instructions: Solve the exercises on exponents and powers below. The answers are given in the next section. You may wish to view the examples on the rules for exponents and powers in the next section first.

1)   a³ × a⁴ = ?

2)   (y²)⁴ = ?

3)   (3x²)(6x⁶) = ?

4)   \(\frac {3^8}{3^5} =  ?\)

5)   Express as a fraction:

6)   Express as a radical:

7)   a × b⁰ = ?

8)   x² × x³ × x⁵= ?

9)   [(x²)⁴]³ = ?

10)   (5ab⁵)(–6ab³) = ?

Exponents and Powers – Answers

1)   The correct answer is:   a⁷

a³ × a⁴ = a^{3 + 4} = a⁷

2)   The correct answer is:   y⁸

(y²)⁴ = y^{2 x 4} = y⁸

3)   The correct answer is:   18x⁸

(3x²)(6x⁶) = (3 × 6)(x^{2 + 6})= 18x⁸

4)   The correct answer is:   27

\(\frac {3^8}{3^5} =\)

3⁸ ÷ 3⁵ =

3^{8 – 5} =

3³ =

3 × 3 × 3 = 27

5)    The correct answer is as follows:

6)    The correct answer is as follows:

7)   The correct answer is:   a

a × b⁰ = a × 1 = a

8)   The correct answer is:   x¹⁰

x² × x³ × x⁵ = x^{2 + 3 + 5} = x¹⁰

9)   The correct answer is:   x²⁴

[(x²)⁴]³ = x^{2 x 4 x 3} = x²⁴

10)   The correct answer is:   -30a²b⁸

(5ab⁵)(–6ab³) = (5 × -6)(a × a)(b^{5 + 3}) = -30a²b⁸

Exponents – Definitions

An exponent shows how many times a number is to be multiplied times itself.

The number or variable is called the base.

A number or variable with an exponent is raised to the power of the exponent.

So, a⁴ is expressed verbally as “a to the power of 4.”

Exponents and Powers – Rules

Same base numbers with different exponents

5² × 5⁷ = ?

The base number for the equation above is 5.

If your base number is the same, you add the exponents when you multiply.

5² × 5⁷ = 5^{(2 + 7)} = 5⁹ = 1,953,125

Remember:  Don’t confuse multiplication with addition.  The result is completely different.

5² + 5⁷ = 25 + 78, 125 = 78,150

Base numbers with a common variable

(2x²)(–4x⁴) = ?

If the base numbers have a common variable and you need to multiply them, multiply the numbers in front of the variable, and add the exponents.

(2x²)(–4x⁴) = –8x⁶

Exponent raised to a power

When you have an exponent raised to a power, you can multiply the exponents.

(x³)² = x⁶

Fraction as exponent

You may see numbers that have fractions in the exponent.

Put the base number inside the radical sign.

The denominator of the fraction in the exponent becomes the root of the radical.

The numerator of the fraction in the exponent is the new exponent.

Fractions that have exponents

\(\frac {x^9}{x^5} = ?\)

On your exam, there may be questions that have factions with exponents in both their numerator and denominator.

Perform division and subtract the exponents when the base number is the same.

\(\frac {x^9}{x^5} =\)

x⁹ ÷ x⁵ = x^{9 – 5} = x⁴

Negative exponents

When you see a negative exponent, you remove the negative sign on the exponent by expressing the number as a fraction, with 1 as the numerator.

Zero exponent

When the base is not equal to zero, any number or variable to the power of zero is equal to 1.

a⁰ = 1

Now try to memorize the exponent rules above.

Exponent Calculator

If you have any questions on exponents that have not been answered in this post, you can try using the exponent calculator.

Exponent Calculator

You may also want to view our posts on:

Polynomials

Quadratics

More Alegbra Practice

Go to the next exercise

Get the download

Solving Equations – Steps for Elimination Method

For examples on solving equations with steps for the elimination method, please look at the examples after the quiz below.

Solving Equations Quiz with Steps & Examples

Instructions: Exercises on solving equations using the steps for the elimination method are included in this quiz. Answer each question and check your answers

[WpProQuiz 9]

Solving Equations – Elimination Method Example

Solving equations with the steps for the elimination method will really be useful for your algebra exam.

Systems of equations are also called simultaneous equations.

We need to use the steps for elimination method when the coefficients on the variables in the system of equations are not the same.

You will remember from our post on algebraic terms that coefficients are the number part of a term.

Look at the example below.

Solving Equations – Steps for Elimination Method

Look at the example below on solving equations and then study the steps that follow on how to carry out the elimination method.

Example:  Solve the system of equations for x and y.

8x – 3y = 30

3x + y = 7

Answer:  x = 3 and y = –2

STEP 1:  Check the equations

Check to see if the equations you are solving have a term with a common coefficient.

Our first equation has 8x and the second equation has 3x, so the coefficients are 8 and 3.

The first equation has 3y and the second equation has y, so the coefficients are 3 and 1.

By comparing the equations in this way, we can see that we do not have any terms with common coefficients.

STEP 2:  Check the algebraic terms

Then determine which equation and which term to perform multiplication on.

We can perform multiplication on the “y” variable in the second equation.

That is because the first equation has 3y and the second equation has y.

So. we can multiply the y in the second equation by 3 in order to get 3y.

STEP 3:  Perform multiplication

Perform multiplication on the equation you chose in step 2.

Our second equation was:  3x + y = 7

Multiply each term in the second equation by 3 as show below.

(3x × 3) + (y × 3) = (7 × 3)

9x + 3y = 21

You have now created a term (3y) that has a coefficient in common with a term in the other equation.

STEP 4:  Perform the elimination method

Perform the elimination method by adding or subtracting the new equation from step 3.

In this problem, we need to add the equations as show below:

           8x – 3y = 30

      + (9x + 3y = 21)

          17x        =  51

          17x ÷ 17 =  51 ÷ 17

                   x   =   3

STEP 5:  Substitute the value

Now substitute x with its value to solve for y.

We know from the previous step that x = 3.

So, take the first equation and substitute this value.

x = 3

8x – 3y = 30

(8 × 3) – 3y = 30

24 – 3y = 30

24 – 3y + 3y = 30 + 3y

24 – 3y + 3y = 30 + 3y

24 = 30 + 3y

24 – 30 = 30 – 30 + 3y

24 – 30 = 30 – 30 + 3y

24 – 30 = 3y

–6 = 3y

–6 ÷ 3 = 3y ÷ 3

–2 = y

y = –2

So, as you can see from the example above, you can use inverse operations in conjunction with the elimination method in order to add or subtract systems of equations that have common terms.

More Algebra Practice

If you need more algebra practice, try our other free algebra practice problems.

For exercises on solving equations using the steps for the substitution method, go to the next exercise:

Get the math download

What is the FOIL Method for Polynomials?

The FOIL method for polynomials is used in order to multiply quadratics. To see more examples on how to use the FOIL method for polynomials, please view the section below the quiz.

Exercises on Foil Method for Polynomials

Instructions:  Use the FOIL method to expand and simplify the algebraic expressions provided below. When you have finished check and compare your work with the solutions given after each question.

[WpProQuiz 16]

FOIL Method – Example

You will have several questions on quadratics on the algebra part of your math examination.

Many quadratic expressions are the result of multiplying two binomials.

You will remember that binomials are two terms that are separated by the addition or subtraction sign.

In other words, we can use the FOIL method when polynomials or quadratic equation or expression is in its factored form.

Look at the example below:

(2x + 4)(3x – 1)

This example is a quadratic expression in its factored form.

We perform FOIL by multiplying the terms in this order: First, Outside, Inside, Last.

FIRST:

Let’s look at how to multiply the first terms.

(2x + 4)(3x – 1)

2x and 3x are first in each set of parentheses.

So, we multiply them together.

(2x × 3x) = 2 × 3 × x × x = 6x²

OUTSIDE:

Next we need to multiply the “outside” terms.

(2x + 4)(3x – 1)

2x and –1 are on the outside of the sets of parentheses.

Take care to multiply subtracted numbers as negatives in your multiplication.

So, we multiply the “outside” terms together.

(2x × –1) = 2 × –1 × x = –2x

INSIDE:

The next step is to multiply the “inside” terms.

(2x + 4)(3x – 1)

4 and 3x are on the inside of the sets of parentheses.

So, multiply these terms together.

(4 × 3x) = 4 × 3 × x = 12x

LAST:

The last multiplication operation in the FOIL method is to multiply the last terms.

(2x + 4)(3x – 1)

4 and –1 are the last terms in each set of parentheses.

So, multiply the last terms.

(4 × –1) = –4

THEN SIMPLIFY:

After we have carried out the FOIL method, we need to place all of the above results together in a quadratic expression.

The result of our “First” multiplication was:   6x²

The result of our “Outside” multiplication was:   –2x

The result of our “Inside” multiplication was:  12x

The result of our “Last” multiplication was:   –4

So, put all of these terms together in a new expression:

6x² + –2x + 12x + –4

The final step is add like terms together to simplify:

6x² + –2x + 12x + –4 =

6x² – 2x + 12x – 4 =

6x² + 10x – 4

Further Algebra Exercises

You should also look at our posts on quadratics, as well as our other algebra practice problems.

Get the download

Completing the Square – Method & Equation

The completing the square method means that we transform a quadratic equation in the usual form of x² + 2bx + c and put it in this format: (x + b)² – b² + c

So, the completing the square equation is:

x² + 2bx + c = (x + b)² – b² + c

Completing the Square Equation – Exercises

Instructions:  Use the completing the square method to write the following quadratic equations in the completed square form. Then solve for x.

1)   x² + 6x + 4 = 0

2)   x² – 8x + 1 = 0

3)   x² – 4x + 15 = 0

4)   2x² + 8x – 3 = 0

5)   3x² – 6x – 7 = 0

Completing the Square Equation – Answers

1)   The correct answer is: \(\text{x = }-\text{3} \pm \sqrt{5}\)
STEP 1:  Expand the equation to identify variables b and c.
Our equation x² + 6x + 4 = 0  is in the format x² + 2bx + c.
x² + (2 × 3 × x) + 4 = x² + 2bx + c
b = 3 and c = 4
STEP 2:  Put the equation in the format (x + b)² – b² + c
(x + 3)² – 3² + 4
STEP 3:  Perform the operations to simplify.
(x + 3)² – 3² + 4 = 0
(x + 3)² – 9 + 4 = 0
(x + 3)² – 5 = 0
(x + 3)² – 5 + 5 = 0 + 5
(x + 3)² = 5
STEP 4:  Take the square root of each side and simplify to solve.
(x + 3)² = 5
\(\sqrt{(x + 3)^2} = \pm \sqrt{5}\)
\(\text{(x + 3) = } \pm \sqrt{5}\)
\(\text{x + 3} – 3 = \pm \sqrt{5} – \text{3}\)
\(\text{x = }-\text{3} \pm \sqrt{5} \)

2)   The correct answer is:  \(\text{x = }\text{4} \pm \sqrt{15} \)
STEP 1:  Expand the equation to identify variables b and c.
Our equation x² – 8x + 1 = 0  is in the format x² + 2bx + c.
x² + (2 × –4 × x) + 1 = x² + 2bx + c
b = –4 and c = 1
STEP 2:  Put the equation in the format (x + b)² – b² + c
(x – 4)² – (–4)² + 1
STEP 3:  Perform the operations to simplify.
(x – 4)² – (–4)² + 1 = 0
(x – 4)² – 16 + 1 = 0
(x – 4)² – 15 = 0
(x – 4)² – 15 + 15 = 0 + 15
(x – 4)² = 15
STEP 4:  Take the square root of each side and simplify to solve.
(x – 4)² = 15
\(\sqrt{(x – 4)^2} = \pm \sqrt{15}\)
\(\text{(x} – 4) = \pm \sqrt{15}\)
\(\text{x} – 4 + 4 = \pm \sqrt{15} + \text{4}\)
\(\text{x = 4} \pm \sqrt{15} \)

3)   The correct answer is:  \(\text{x = 2} \pm \sqrt{-11} \)
STEP 1:  Expand the equation to identify variables b and c.
Our equation x² – 4x + 15 = 0  is in the format x² + 2bx + c.
x² + (2 × –2 × x) + 15 = x² + 2bx + c
b = –2 and c = 15
STEP 2:  Put the equation in the format (x + b)² – b² + c
(x – 2)² – (–2)² + 15
STEP 3:  Perform the operations to simplify.
(x – 2)² – (–2)² + 15 = 0
(x – 2)² – 4 + 15 = 0
(x – 2)² + 11 = 0
(x – 2)² + 11  – 11 = 0  – 11
(x – 2)² =  –11
STEP 4:  Take the square root of each side and simplify to solve.
(x – 2)² = –11
\(\sqrt{(x – 2)^2} = \pm \sqrt{-11}\)
\(\text{(x} – 2) = \pm \sqrt{-11}\)
\(\text{x} – 2 + 2 = \pm \sqrt{-11} + \text{2}\)
\(\text{x = 2} \pm \sqrt{-11} \)

4)   The correct answer is: \(\text{x =} – 2 \pm \sqrt{\frac{11}{2}} \)
STEP 1:  Expand the equation to identify variables a, b, and c.
\(\text{ax}^{2} + bx + c = a\bigg(x + \frac{b}{2a}\bigg)^{2}+ d\)
Our equation 2x² + 8x – 3 = 0  is in the format ax² + bx + c.
2x² + (8 × x) – 3 = 0
a = 2     b = 8     c = –3
STEP 2:  Expand the equation in squared form to calculate variable d.
(i) Divide variable b by variable a:   8 ÷ 2 = 4
(ii) Divide the previous calculation by 2:   4 ÷ 2 = 2
(iii) Use the result from (ii) as the second term in the parentheses to factor the quadratic: 2(x + 2)²
(iv) Simplify to calculate d:
2(x + 2)² =
2(x + 2)(x + 2) =
[2(x × x) + (x × 2) + (2 × x) + (2 × 2)] =
[2(x² + 4x + 4)] =
2x² + 8x + 8  We deduct this number from c to get d.
c = –3   d = –3 – 8 = –11
STEP 3:  Put the equation in the format \(\text{a}\bigg(x + \frac{b}{2a}\bigg)^{2}+ d\)
a = 2     b = 8     d = –11
\(\text{2}\bigg(x + \frac{8}{2 \times 2}\bigg)^{2}+ -11\)
STEP 4:  Perform the operations to simplify.
\(\text{2}\bigg(x + \frac{8}{2 \times 2}\bigg)^{2}+ -11\)
\(\text{2}\bigg(x + \frac{8}{4}\bigg)^{2}+ -11\)
2(x + 2)² – 11 = 0
2(x + 2)² – 11 + 11 = 0 + 11
2(x + 2)² = 11
[2(x + 2)² ÷ 2] = 11 ÷ 2
\(\text{(x + 2)}^{2} = \frac{11}{2}\)
STEP 5:  Take the square root of each side and simplify to solve.
\(\text{(x + 2)}^{2} = \frac{11}{2}\)
\(\sqrt{(x + 2)^2} = \pm \sqrt{\frac{11}{2}}\)
\(\text{(x} + 2) = \pm \sqrt{\frac{11}{2}}\)
\(\text{x} + 2 – 2 = \pm \sqrt{\frac{11}{2}} – \text{2}\)
\(\text{x =} – 2 \pm \sqrt{\frac{11}{2}} \)

5)   The correct answer is:  \(\text{x =} 1 \pm \sqrt{\frac{10}{3}} \)
STEP 1:  Expand the equation to identify variables a, b, and c.
\(\text{ax}^{2} + bx + c = a\bigg(x + \frac{b}{2a}\bigg)^{2}+ d\)
Our equation 3x² – 6x – 7 = 0 is in the format ax² + bx + c.
3x² + (–6 × x) – 7 = 0
a = 3     b = –6     c = –7
STEP 2:  Expand the equation in squared form to calculate variable d.
(i) Divide variable b by variable a:   –6 ÷ 3 = –2
(ii) Divide the previous calculation by 2:   –2 ÷ 2 = –1
(iii) Use the result from (ii) as the second term in the parentheses to factor the quadratic: 3(x – 1)²
(iv) Simplify to calculate d:
3(x – 1)² =
3(x – 1)(x – 1) =
[3(x × x) + (x × –1) + (–1 × x) + (–1 × –1)] =
[3(x² – 2x + 1)] =
3x² – 6x + 3  We deduct this number from c to get d.
c = –7   d = –7 – 3 = –10
STEP 3:  Put the equation in the format \(\text{a}\bigg(x + \frac{b}{2a}\bigg)^{2}+ d\)
a = 3     b = –6     d = –10
\(\text{3}\bigg(x + \frac{-6}{2 \times 3}\bigg)^{2}+ -10\)
STEP 4:  Perform the operations to simplify.
\(\text{3}\bigg(x + \frac{-6}{2 \times 3}\bigg)^{2}+ -10\)
\(\text{3}\bigg(x + \frac{-6}{6}\bigg)^{2}+ -10\)
3(x – 1)² – 10 = 0
3(x – 1)² – 10 + 10 = 0 + 10
3(x – 1)² = 10
[3(x – 1)² ÷ 3] = 10 ÷ 3
\(\text{(x – 1)}^{2} = \frac{10}{3}\)
STEP 5:  Take the square root of each side and simplify to solve.
\(\text{(x – 1)}^{2} = \frac{10}{3}\)
\(\sqrt{(x – 1)^2} = \pm \sqrt{\frac{10}{3}}\)
\(\text{x} – 1 = \pm \sqrt{\frac{10}{3}}\)
\(\text{x} – 1 + 1 = \pm \sqrt{\frac{10}{3}} + \text{1}\)
\(\text{x =} 1 \pm \sqrt{\frac{10}{3}} \)

Completing the Square Method – Example

Let’s look at an example problem that illustrates the completing the square method.

Write x² + 6x + 20 in the form (x + b)² – b² + c

STEP 1: Identify variables b and c.

Our equation x² + 6x + 20  is in the format x² + 2bx + c.

Expand the equation to identify b:

x² + (2 × 3 × x) + 20 = x² + 2bx + c

So, b = 3 and c = 20

STEP 2: Put the equation in the format (x + b)² – b² + c

When b = 3 and c = 20

(x + 3)² – 3² + 20

STEP 3: Perform the operations to simplify.

(x + 3)² – 3² + 20 =

(x + 3)² – 9 + 20 =

(x + 3)² + 11

STEP 4: You may check your answer by performing the multiplication using the FOIL method.

(x + 3)² + 11 =

(x + 3)(x + 3) + 11 =

[(x × x) + (x × 3) + (3 × x) + (3 × 3)] + 11 =

x² + 3x + 3x + 9 + 11 =

x² + 6x + 20 (which was our original equation)

Completing the Square – Solving for x

Let’s look at our equation from step 3 above.

To solve for x, first we have to move the spare number to the other side.

(x + 3)² + 11 = 0

(x + 3)² + 11 – 11 = –11

(x + 3)² = –11

Then take the square root of each side and simplify to solve.

(x + 3)² = –11

\(\sqrt{(x + 3)^2} = \pm \sqrt{-11}\)

\(\text{(x + 3) = } \pm \sqrt{-11}\)

\(\text{x + 3} – 3 = \pm \sqrt{-11} – \text{3}\)

\(\text{x = } \pm \sqrt{-11} – \text{3}\)

\(\text{x = }- \text{3} \pm \sqrt{-11}\)

We always need to put the plus-minus symbol in front of the square root symbol on the right side of the equation when we solve for x.

The square root of a negative number is always an imaginary number, so we would be to use variable i to simplify the problem further.

Completing the Square – Advanced Problems

If you have an advanced math part on your algebra test, you will need to know the following formula for the advanced completing the square method:

\(\text{ax}^{2} + bx + c = a\bigg(x + \frac{b}{2a}\bigg)^{2}+ d\)

You have to do a separate calculation to determine what value to subtract from variable c in order to get variable d.

Completing the Square and Quadratic Graphs

Quadratic equations appear as curves when plotted on a graph.

All quadratic graphs will have a minimum point at the bottom of the curve.

Completing the square can also be used in order to find the x and y coordinates of the minimum value of a quadratic equation on a graph.

We cover how to graph quadratics in more depth in our graphing posts.

You may also want to try our other free algebra problems.

What are Double Sided Equations?

Double sided equations have an unknown on both sides. This means that  you will see the same variable on both sides of the equation.

Double Sided Equations – Exercises

Instructions:  Solve for the unknown variable in the following questions. You may want to see the examples below the quiz first.

[WpProQuiz 8]

Example

Double sided equations may contain constants, which are usually whole numbers or fractions.

They will also have terms that contain variables, such as x or y, and coefficients, which are the number part of the term.

Look at the following example of how to solve double sided equations.

Example:  Solve for y:  2y + 4 = y + 3

Answer:  y = –1

STEP 1:  Deal with the constants first.

2y + 4 = y + 3

2y + 4 – 4 = y + 3 – 4

2y + 4 – 4 = y + 3 – 4

2y = y – 1

STEP 2:  Get the variables to one side of the equation.

2y = y – 1

2y – y = y – y – 1

2y – y = y – y – 1

y = –1

STEP 3:  For advanced problems, you may need to perform further operations, such as multiplication or division.

You may also see advanced questions that involve shapes or figures.

Further Algebra Exercises

For more free practice problems, please visit our algebra practice page.

If you are taking the advanced part of the algebra test, you should also try our exercises on quadratics.

Balancing Algebraic Equations – Practice Problems

If you are looking for balancing algebraic equations practice problems in math, please go to the next section below. If you need to see the examples first, please scroll down to the second half of the page.

Instructions:  

Balance the following equations as indicated in each question. Express your answer as a simplified fraction, if possible.

1)   If A + B – C = D, then A = ?

2)   If (W + X) ÷ Y = Z, then X = ?

3)   If 5a + 3b = c, then a = ?

4)   \(\text {If  x = } \frac{yv}{w} \text {, then w = ?}\)

5)   \(\text {If } \frac{JKL}{M}  \text { + N = P, then K = ?}\)

Balancing Equations Practice – Answers

Answer 1

1)   The correct answer is:  A = D + C – B

If A + B – C = D, then A = ?

A + B – C = D

A + B – C + C = D + C

A + B – C + C = D + C

A + B – B = D + C – B

A + B – B = D + C – B

A = D + C – B

Answer 2

2)   The correct answer is: X = ZY – W

If (W + X) ÷ Y = Z, then X = ?

(W + X) ÷ Y = Z

(W + X) ÷ Y × Y = Z × Y

(W + X) ÷ Y × Y = Z × Y

W + X = ZY

W – W + X = ZY – W

W – W + X = ZY – W

X = ZY – W

Answer 3

3)   The correct answer is:  \(\text {a = } \frac{c – 3b}{5}\)

If 5a + 3b = c, then a = ?

5a + 3b = c

5a + 3b – 3b = c – 3b

5a + 3b – 3b = c – 3b

5a = c – 3b

5 × a = c – 3b

5 ÷ 5 × a = c – 3b  ÷ 5

5 ÷ 5 × a = c – 3b  ÷ 5

a = c – 3b  ÷ 5

\(\text {a = } \frac{c – 3b}{5}\)

Answer 4

4)   The correct answer is:  \(\text {w = } \frac{yv}{x} \)

\(\text {If  x = } \frac{yv}{w} \text {, then w = ?}\)

\(\text {x = } \frac{yv}{w}\)

\(\text {x = yv} \div w\)

\(\text {x} \times \text {w = yv}  \div \text {w} \times \text {w}\)

\(\text {xw = yv}\)

\(\text {xw} \div \text {x = yv} \div \text {x}\)

\(\text {w = } \frac{yv}{x} \)

Answer 5

5)   The correct answer is:  \(\text { K = } \frac{MP – MN}{JL}\)

\(\text {If } \frac{JKL}{M}  \text { + N = P, then K = ?}\)

\(\frac{JKL}{M}  \text { + N = P}\)

\(\frac{JKL}{M}  \text { + N} – N = P – N\)

\(\frac{JKL}{M}  \text { = P} – N\)

\(\text {JKL} \div  \text {M}  = P – N\)

\(\text {JKL} \div  \text { M} \times \text {M} = (P – N) \times \text {M}\)

\(\text {JKL} \text { = } (P – N) \times \text {M}\)

\(\text {JL} \times \text { K} = (P – N) \times \text {M}\)

\(\text {JL} \div \text {JL} \times \text { K} = (P – N) \times \text {M} \div \text {JL}\)

\(\text { K} = (P – N) \times \text {M} \div \text {JL}\)

\(\text { K} = (MP – MN) \div \text {JL}\)

\(\text { K = } \frac{MP – MN}{JL}\)

What is “Balancing Equations” in Math?

“Balancing equations” means that you can perform any operation on one side of an algebraic equation if you perform the exact same operation on the other side of the equation. You will need to balance equations in order to “undo” operations to solve the problem.

Balancing Equations with Binary Operations

The phrase “binary operations” also means that whatever operation you do to one side of an equation, you need to do the exact same operation on the other side of the equation.

Balancing equations with binary operations refers to addition, subtraction, multiplication, and division.

After you balance the equation, you can cancel out by drawing a line through the inverse operations as shown in the examples below.

Examples:

Balancing Algebraic Equations with Addition & Subtraction

Look at the examples below on how to balance equations by using addition and subtraction.

Example 1:  Solve by adding

The problem below has the minus sign. So to solve we need to do the opposite operation; in other words, we have to add back to solve.

Solve for x by adding 10 to each side.

x – 10 = 56

x – 10 + 10 = 56 + 10

x – 10 + 10 = 56 + 10

x = 66

Example 2:

The problem below has the plus sign. So to solve we need to do the opposite operation; so, we have to subtract to solve.

Solve for y by subtracting 15 from each side.

y + 15 = 45

y + 15 – 15 = 45 – 15

y + 15 – 15 = 45 – 15

y = 30

Balancing Equations Practice- Multiplying Each Side by the Same Number

Look at the example below on how to balance equations by using multiplication

Example 3:   Solve by Multiplying

The problem below has the divide sign. Remember that to solve, we always need to do the opposite operation; so in this case, we have to multiply to solve the problem.

Solve for a by multiplying each side by 2

a ÷ 2 = 11

a ÷ 2 × 2 = 11 × 2

a ÷ 2 × 2 = 11 × 2

a = 22

Balancing Equations Practice – Dividing Each Side by the Same Number

The problems below has the minus sign. So to solve we need to do the opposite operation; in other words, we have to add back to solve.Look at the example below on how to balance equations by using division.

Example 4:  

The problem below has the times sign. So to solve we need to divide to undo the multiplication.

Your first step is to divide each side by 6.

5b × 6 = 90

5b × 6 ÷ 6 = 90 ÷ 6

5b × 6 ÷ 6 = 90 ÷ 6

5b = 90 ÷ 6

Now we have to get rid of the 5 in front of the b, so now we have to divide each side by 5.

5b = 90 ÷ 6

5 × b = 90 ÷ 6

5 ÷ 5 × b  = 90 ÷ 6 ÷ 5

5 ÷ 5 × b  = 90 ÷ 6 ÷ 5

b = 90 ÷ 6 ÷ 5

b = 3

Balancing Equations on the Maths Exam

For problems on your exam, you will usually have to perform more than one operation in order to balance the equation.

If you found the above exercises difficult you may want to look at the following posts:

Fractions

Solving Algebraic Equations

More Free Algebra Problems

PDF Downloads

Algebraic Terms Definition

To identify algebraic terms, the definition of the word terms is needed first of all. In algebra, terms are separated by a plus or minus sign in an expression.

For an in-depth explanation, please scroll down.

Terms of an Algebraic Expression – Exercises

Instructions:  Consider algebraic terms below and answer the questions that follow. You may want to see the explanations below first.

4a² + 16ab + 24b⁴ – 8

1)   Is the above statement an expression, equation, or inequality?

2)   Identify the variables.

3)   Identify the coefficients.

4)   Identify the constant.

5)   Identify the greatest common factor and express in factored form.

Terms of an Algebraic Expression – Answers

1)   The statement is an expression since it does not have the equals sign.

It also does not have the greater than or less than sign.

2)   The variable in the first term is a.

The variables in the second term are a and b.

The variable in the third term is b.

3)   The coefficient in the first term is 4.

The coefficient in the second term is 16.

The coefficient in the third term is 24.

4)   The constant is –8.

5)   The greatest common factor is 4. Factor as shown below.

4a² + 16ab + 24b⁴ – 8 =

(4 × a²) + (4 × 4 × ab) + (4 ×  6 × b⁴) + (4 × –2) =

4[(4 × a²) + (4 × 4 × ab) + (4 ×  6 × b⁴) + (4 × –2)] =

4(a² + 4ab + 6b⁴ – 2)

What are Algebraic Terms?

Algebraic terms are used to form algebraic expressions.

Algebraic terms consist of variables, coefficients, exponents, and constants.

Algebraic Terms Are Separated by Signs

Algebraic terms are separated by the addition or subtraction signs.

Variables:  Variables are the letters, such as x or y, in an algebraic expression.

Coefficients:  Coefficients are the numbers directly in front of the variables, such as the 4 in the term 4x² or the 7 in the term 7y³.

Exponents:  Exponents are the powers in an algebraic expression, such as the 2 in the term 4x² or the 3 in the term 7y³.

Constants:  Constants are the numbers without variables in an algebraic expression.

Terms can be used to create expressions, equations, and inequalities in algebra.

Expressions:  Expressions are used to create equations and inequalities in algebra.

Equations:  An algebraic equation must have the equals sign.

Inequalities:  An algebraic inequality must have the less than or greater than sign.

Algebraic Terms Separated By the Plus Sign – Examples

Here is an algebraic expression:

4x² + 7y³ + 3

If we add an equals sign and a value we get an algebraic equation:

4x² + 7y³ + 3 = 0

If we add the less than or greater than sign and a value to our algebraic expression we get an algebraic inequality:

4x² + 7y³ + 3 < 5

Algebraic Terms Separated By the Plus and Minus Signs – Examples

Look at the following algebraic expression as an illustration of algebraic terms.

3x² + 9xy + 15y³ – 6

The first algebraic term is 3x².

It consists of the variable x, the coefficient 3, and the exponent 2.

The second algebraic term is 9xy.

It consists of the variable x, the variable y, and the coefficient 9.

The third algebraic term is 15y³

It consists of the variable y, the coefficient 15, and the exponent 3.

The fourth algebraic term is –6.

The fourth term is a constant since it does not contain a variable.

Remember that you can identify your term as a negative if the term is preceded by the minus sign.

How to factor terms in algebraic expressions

You will also need to know how to factor expressions and equations by finding common factors in the algebraic terms.

In order to factor our equation, we take out the greatest common factor as shown below:

3x² + 9xy + 15y³ – 6 =

3(x² + 3xy + 5y³ – 2)

Terms of Algebraic Expressions – Further Practice

If you do not understand how to perform the operation illustrated above, you should also view the following posts.

Grouping Like Terms

Finding the Greatest Common Factor

Factoring Expressions

Algebraic terms are also used to create quadratic expressions.

You should also view our posts on binomials, trinomials, and polynomials.

Distributive Property of Multiplication with Fractions and Variables – Free Exercises

Instructions: Below you will find free exercises on the distributive property of multiplication with fractions and variables. The answers and explanations are given in the next section. If you want to see the examples first, please scroll down.

1)   6(4x + 7y + 5) = ?

2)   Perform the operation: 5(2x – 8y + 4)

3)   Simplify: 4(3x + 2x + 4y + 5y + 3 + 7)

4)   –7(3x – 6y + 4) = ?

5)  Simplify the equation that follows:

Answers to the Distributive Property with Fractions and Variables Exercise

Problem 1:

Perform the distributive property of multiplication with the variable by multiplying each item inside the parentheses by 6 as shown below:

6(4x + 7y + 5) =

(6 × 4x) + (6 × 7y) + (6 ×5) =

24x + 42y + 30

Problem 2:

Multiply each item inside the parentheses by 5 as shown below:

5(2x – 8y + 4) =

(5 × 2x) – (5 × 8y) + (5 × 4) =

10x – 40y + 20

Problem 3:

Add the like terms together as shown below:

4(3x + 2x + 4y + 5y + 3 + 7) =

4(5x + 9y + 10)

Then carry out the distributive property by multiplying the terms, variables or integers inside the parentheses by 4.

4(5x + 9y + 10) =

(4 × 5x) + (4 × 9y) + (4 × 10) =

20x + 36y + 40

Problem 4:

Be careful with the negative sign when you multiply in this problem.

–7(3x – 6y + 4) =

(–7 × 3x) + (–7 × –6y) + (– 7 × 4) =

–21x + 42y – 28

Problem 5:

Here we have a problem on the distributive property with fractions.

Distributive Property of Multiplication – Step by Step

The distributive property of multiplication with variables and fractions is performed when the variable or number in front of a set of parentheses is multiplied by each item inside the parentheses.

The “items” within this type of algebra problem are called terms.

A term consists of a variable, number, or variable and number combination.

All of the following are examples of terms:

a

4

xy

5b

Terms also include decimals and fractions. Terms can be positive as well as negative.

Algebraic Distribution – Example

You might see a question like the following one on your entrance exam:

Distribute the number 3 over the terms 5x + 2y + 3

Remember that the word “distribute” means multiply.

STEP 1: Set up the problem in equation form.

3(5x + 2y + 3)

STEP 2: Multiply each term inside the parentheses by the term in front of the parentheses.

(3 × 5x) + (3 × 2y) + (3 × 3)

STEP 3: Perform the multiplication to solve.

(3 × 5x) + (3 × 2y) + (3 × 3) =

15x + 6y +9

Tip: Add Before Distributing

Check to see if any of the terms inside the parentheses can be added together before you do the multiplication.

You can add numbers together and variables together.

For example: 2(2x + 3x + 2 + 5) = ?

2(2x + 3x + 2 + 5) =

2(5x + 7) =

10x + 14

Distribution of Negatives

If the term in front of the parentheses is negative, each term inside the parentheses has to change its sign.

This means that positive terms inside the parentheses become negative, and negative terms become positive.

Look at this example:

−5(6x − 3y + 4) =

(−5 × 6x) + (−5 × −3y) + (−5 × 4) =

−30x + 15y − 20

Instructions on Distribution Problems

As shown above, the instructions to your problem may tell you to distribute a number over the terms.

You may also see instructions that are worded slightly differently, like the following examples.

Simplify:

Perform the operation:

3(2x + 3y)= ?

In the last example, the question mark indicates that you need to perform algebraic distribution.

Distribution – More Help

If you have had difficulties solving the above problem, please visit our pages on fractions and finding the lowest common denominator.

We will look at distribution again in our post on exponent properties.

Algebra Practice Questions

Exam SAM on YouTube

Algebra Equations for Beginners – Exercises

Here are some exercises on math, with algebra equations for beginners. If you want to see the examples first, please scroll down.

Instructions: Find the value of the variable in the following equations. Your answer may be a whole number, a decimal, or a fraction.

1)   5(x – 1) = 20

2)   4x + 3 = 9

3)  \(\frac{3x – 5}{2} = 10\)

4)   x³ + 5 = 32

5)   \(\sqrt{x} + 7 = 15\)

Algebra Equations for Beginners – Answers

Answer 1

1)   The correct answer is:  x = 5

Expand the equation:

5(x – 1) = 20

(5 × x) + (5 × –1) = 20

5x – 5 = 20

Deal with the integer.

5x – 5 + 5 = 20 + 5

5x = 25

Divide by the coefficient to solve.

5x ÷ 5 = 25 ÷ 5

x = 5

Answer 2

2)  The correct answer is:  x = 3/2 or x = 1.5

Deal with the integer.

4x + 3 = 9

4x + 3 – 3 = 9 – 3

4x = 6

Divide by the coefficient to solve.

4x ÷ 4 = 6 ÷ 4

\(\text x =  \frac{6}{4} =  \frac{3}{2} = 1.5\)

Answer 3

3)  The correct answer is:  x = 25/3

Eliminate the fraction by multiplying each side by the denominator.

\(\frac{3x – 5}{2} = 10\)

\(\frac{3x – 5}{2} \times 2 = 10 \times 2\)

3x – 5 = 20

Deal with the integer.

3x – 5 + 5 = 20 + 5

3x = 25

Divide by the coefficient to solve.

3x ÷ 3 = 25 ÷ 3

\(\text x = \frac{25}{3}\)

Answer 4

4)   The correct answer is: x = 3

Deal with the integer.

x³ + 5 = 32

x³ + 5 – 5 = 32 – 5

x³ = 27

Find the cube root of each side to solve.

\(\sqrt[3]{x^3} = \sqrt[3]{27}\)

3 × 3 × 3 = 27

x = 3

Answer 5

5)   The correct answer is: x = 64

Deal with the integer.

\(\sqrt{x} + 7 = 15\)

\(\sqrt{x} + 7 – 7 = 15 – 7\)

\(\sqrt{x} = 8\)

Square each side to solve

\(\sqrt{x}^2 = 8^2\)

8² = 64

x = 64

Algebra equations for beginners, both with and without parentheses, are included on almost all college placement tests and on many educator licensing examinations.

You should study the algebra equations with parentheses on this page if you need more help on that part of your math test.

What are Algebra Equations?

There are many different types of algebra equations.

To see practice problems on one-sided equations, please go to the bottom of this page.

One-Sided Algebra Equations – Example

To solve one-sided algebra equations, we need to isolate the variable to one side of the equation by performing operations on the other numbers.

You may need to add, subtract, divide, or multiply the other numbers in a one-sided algebra equation.

The basic concept is that you can perform any operation on one side of the equation if you perform the exact same operation on the other side of the equation.

Example:   If 3x – 7 = 8, what is the value of x?

Answer:   x = 5

STEP 1: Deal with the integers first.

Add 7 to each side:

3x – 7 = 8

3x – 7 + 7 = 8 + 7

3x = 15

STEP 2:  Deal with the coefficients (the numbers in front of the variables) to solve.

Divide each side by 3:

3x ÷ 3 = 15 ÷ 3

x = 5

To see examples of how to solve equations that have a variable on each side, please see our post entitled “double-sided equations.”

Algebra Equations – Problem Solving Methods

This post has shown only some very brief examples on solving equations on the algebra part of your test.

Our blog also has posts on how to deal with binomials, trinomials, and other types of polynomials.

You will also see posts on how to set up equations, as well as on how to solve equations.

We provide examples of different problem solving methods for practical problems on your exam.

For help with algebra equations with parentheses, please see our posts on:

Balancing equations

Inverse Operations

You can also try our pre-algebra review and our algebra exercises.

Subscribe to Us on YouTube

Solving Absolute Value Equations on Both Sides of the Equation

This page gives exercises and examples on solving absolute value equations on both sides of the equation. The exercises are in the next section.

In case you want to see the examples on solving absolute value equations on both sides first, go to the middle of the post for the examples and explanations.

Absolute Value – Exercises

1) If | x + y | = 5 and x = 3, then what is a possible value of y ?

2) What is the value of | xy | when x = –10 and y = 14?

3) If x = 8 and the value of | x ÷ y | = 0, then what is a possible value of y?

4) If x = –7 and | x | = y, then what is a possible value of y?

5) If y = 8 and | x | = y, what is a possible value of x?

Absolute Value Problems – Answers

Answer 1

1) The correct answer is:   y = 2 and y = –8

If | x + y | = 5 and x = 3, we can substitute 3 for the value of x to solve.

| x + y | = 5

| 3 + y | = 5

| 3 + 2 | = 5

y = 2

However, for absolute value problems, you also have to consider other possible values. If | x + y | = 5 then | x + y | = | –5 | We know this because the absolute value of –5 is 5. So again substitute for the value of x to solve.

| x + y | = | –5 |

| 3 + y | = | –5 |

| 3 + –8 | = | –5 |

So, the possible values of y are –8 and 2.

Answer 2

2) The correct answer is: 140

What is the value of | xy | when x = –10 and y = 14?

Substitute the values to solve. | xy | = | –10 × 14 | = | – 140 | = 140

Answer 3

3) The answer is: no real number

If x = 8 and the value of | x ÷ y | = 0, then what is a possible value of y?

This could be considered a trick question. It is impossible to divide 8 by any real number that would result in zero as the answer.

Answer 4

4) The answer is: y = 7

If x = –7 and | x | = y, then what is a possible value of y?

| x | = y

| –7 | = y

7 = y

Answer 5

5) The answer is: x = –8 or x = 8

If y = 8 and | x | = y, what is a possible value of x?

| x | = y

| x | = 8

x = –8 or x = 8

Solving Absolute Value Equations on Both Sides – Explanations

Absolute value equations look like the following:

| –3 + 5 – 8 | = ?

For absolute value problems, you will see numbers, variables, or terms between the symbols |  |.

The symbol means that you have to simplify the expression and then give the result as a positive number or variable.

So, the results of absolute value equations will always be positive.

Absolute Value — Example

Let’s look at our example problem again:  | –3 + 5 – 8 | = ?

To solve the equation, perform these steps.

Step 1:

Simplify the equation inside the absolute value symbols.

–3 + 5 – 8 =

5 – 8 – 3 =

5 – 11 =

–6

Step 2:

Express the result as a positive number.

| –6 | = 6

Solving Absolute Value Equations on Both Sides – Advanced Problems

You may also see advanced problems on solving absolute value equations on both sides on your exam.

These types of questions may include algebraic expressions or inequalities.

For example: If x = 2 and y = 3, then | –x + 3y | = ?

Simplify the equation by substituting the values.

| –x + 3y | =

| –2 + (3 × 3) | =

| –2 + 9 | =

| 7 | =

7

Solving Absolute Value Equations on Both Sides – Rules to Remember

Addition

The absolute value of the sum of two numbers will always be less than or equal to the sum of the individual absolute values.

The equation for the addition rule is:

| x + y | ≤ | x | + | y |

Example:

If x = –7 and y = 5

| x + y | ≤ | x | + | y |

| –7 + 5 | ≤ | –7 | + | 5 |

| –2 | ≤  7 + 5

2 ≤ 12

Subtraction

If the absolute value of the difference between two numbers is zero, then the two numbers must be equal.

The equation for the subtraction rule is:

If | x – y | = 0, then x = y

Example:

If x = 3 and y = 3

| 3 – 3 | = 0

0 = 0

Multiplication

The absolute value of the product of two numbers will always be equal to the product of the individual absolute values.

The equation for the multiplication rule is:

| xy | = | x | × | y |

Example:

If x = 4 and y = –8

| xy | = | x | × | y |

| 4 × –8 | = | 4 | × | –8 |

| –32 | = 4 × 8

| –32 | = 32

Division

The absolute value of the quotient of two numbers will always be equal to the quotient of the individual absolute values.

The equation for the division rule is:

| x ÷ y | = | x | ÷ | y |

Example:

If x = 6 and y = –3

| x ÷ y | = | x | ÷ | y |

| 6 ÷ –3 | = | 6 | ÷ | –3 |

| –2 | = 6 ÷ 3

| –2 | = 2

Solving Absolute Value Inequalities

1)  If the absolute value of x is less than or equal to y, then the value of x will always be between the values of negative y and y.

The equation for the first inequality rule is:

If, | x | ≤ y, then –y ≤ x ≤ y

Example:

If x = –9 and y = 12

If | x | ≤ y, then –y ≤ x ≤ y

If | –9 | ≤ 12, then –12 ≤ –9 ≤ 12

2) If the absolute value of x is greater than or equal to y, then the value of x will be less than or equal to the value of negative y or y will be less than or equal to x.

The equation for the second inequality rule is:

If | x | ≥ y, then x ≤ –y  or y ≤ x

Example:

If x = 15 and y = –5

If | x | ≥ y, then y ≤ x

If | 15 | ≥ –5, then –5 ≤ 15

You may also like to look at our posts on math help and geometry.

All Irrational Numbers on Exams

You may see questions asking you to identify the characteristics of all irrational numbers on your algebra test.

Irrational Numbers – Exercises

Instructions:  Simplify the algebraic expressions below as much as possible. Then state whether the result is a rational or irrational number. You may want to view the examples in the next section before attempting the exercise.

1)   5π

2)  13 + \(\sqrt{2}\)

3)  \(\sqrt{3} \times \sqrt{3}\)

4)  \(\sqrt{3} + 7\)


5)  \(\frac{1 \pm \sqrt{2}}{2}\)

6)  \(\sqrt{3} + \sqrt{3}\)

7)  \(\frac{2 \pm \sqrt{3}}{5}\)

8)  1 – \(\sqrt{3}\)

9)   π ÷ 3

10)  \(\sqrt{-1}\)

Irrational Numbers – Answers

1)   The correct answer is:  irrational
5π is an irrational number. When π is multiplied by a rational number like 5, the result is irrational because it will have an infinite number of decimal places.

2)  The correct answer is:  irrational
13 + \(\sqrt{2}\)
13 + \(\sqrt{2}\) is an irrational number. When 13 is added to \(\sqrt{2}\), the result is irrational because it will have an infinite number of decimal places.

3)  The correct answer is:  rational
When simplified, we get 3, which is a rational number.
\(\sqrt{3} \times \sqrt{3} =\)
\(\sqrt{3}^2 = 3\)

4)  The correct answer is:  irrational
\(\sqrt{3} + 7\)
\(\sqrt{3} + 7\) is an irrational number. When 7 is added to \(\sqrt{3}\), the result is irrational because it will have an infinite number of decimal places.

5)  The correct answer is:  irrational
\(\frac{1 \pm \sqrt{2}}{2}\)
The result is irrational because when we multiply \(\sqrt{2}\) by one-half, there is an infinite number of decimal places.

6)  The correct answer is:  irrational
\(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\)
The result is irrational because when we multiply \(\sqrt{3}\) by two, there is an infinite number of decimal places.

7)  The correct answer is:  irrational
\(\frac{2 \pm \sqrt{3}}{5}\)
We cannot simplify the result further without getting an infinite number of decimal places.

8)  The correct answer is:  irrational
1 – \(\sqrt{3}\)
We cannot simplify the result further without getting an infinite number of decimal places.

9)   The correct answer is:  irrational
p ÷ 3
We cannot simplify the result further without getting an infinite number of decimal places.

10)  The correct answer is:  neither rational or irrational
\(\sqrt{-1}\) is an imaginary number because we cannot multiply any real number by itself to get a negative number.

Irrational Numbers – Characteristics

An irrational number is the opposite of a rational number.

In other words, irrational numbers have these characteristics in common: they cannot be expressed as a fraction or as integers.

So, all irrational numbers have non-terminating, non-repeating decimals, when simplified.

Irrational Numbers – π and Square Roots

For example, π is an irrational number.

When expressed as a decimal, π goes to an infinite number of decimal places.

\(\sqrt{2}\) and \(\sqrt{3}\) go to an infinite number of decimal places when expressed as decimal numbers.

So, \(\sqrt{2}\) and \(\sqrt{3}\) are also irrational numbers.

Operations on π

When π is multiplied or divided by a rational number, or added to or subtracted from a rational number, the result is an irrational number.

That is because the result of any operation on π will go to an infinite number of decimal places.

Irrational Numbers – More Examples

Irrational numbers often result from using the quadratic formula or when working with square roots.

However, you always need to be sure that you simplify each expression as much as possible before deciding if the result is rational or irrational.

Look at the examples that follow.

Example 1:

State whether the following is a rational or irrational number.

\(\frac{1 \pm \sqrt{2}}{3}\)

Answer:  Irrational

\(\frac{1 \pm \sqrt{2}}{3}\) is an irrational number because \(\sqrt{2}\) is an irrational number and this fraction cannot be simplified further.

Example 2:

Simplify the following. Then state whether the result is a rational or irrational number.

\(\frac{2}{\sqrt{2}} \times \frac{8}{\sqrt{2}}\)

Answer:  Rational

\(\frac{2}{\sqrt{2}} \times \frac{8}{\sqrt{2}}\) is a rational number because it equals an integer, when simplified.

Study the proof below.

\(\frac{2}{\sqrt{2}} \times \frac{8}{\sqrt{2}} =\)

\(\frac{2 \times 8}{\sqrt{2} \times \sqrt{2}} =\)

\(\frac{16}{\sqrt{2}^2} =\)

\(\frac{16}{2} = 8\)

Example 3:

Simplify the following. Then state whether the result is a rational or irrational number.

\(\frac{3}{\sqrt{2}} + \frac{6}{\sqrt{2}}\)

Answer:  Irrational

\(\frac{3}{\sqrt{2}} + \frac{6}{\sqrt{2}}\) is an irrational number because it has an infinite number of decimal places in the denominator.

Study the proof below.

\(\frac{3}{\sqrt{2}} + \frac{6}{\sqrt{2}} =\)

\(\frac{3 + 6}{\sqrt{2}} =\)

\(\frac{9}{\sqrt{2}}\)

You may want to review our posts on square roots, fractions, and the quadratic formula if you are not familiar with these concepts.

Further Algebra Practice

Irrational numbers should not be confused with imaginary numbers.

If you are taking an advanced algebra exam or college-level math placement test, you may also want to look at our posts on imaginary numbers.

You might also want to study our free algebra practice problems.

Get the downloads