Calculate Surface Area of a Circle Given Radius or Diameter
This page will show you how to calculate the surface area of a circle given radius or diameter.
Study the examples in the sections below before doing the quiz.
Surface Area of a Circle – Quiz
Instructions: Calculate the areas of the circles in each question that follows.
[WpProQuiz 33]
What is Surface Area?
The surface area of a circle is the amount of space on the inside of the circle.
Look at the illustration of a circle below:
The amount of space in the blue part of the circle is the surface area of the circle.
Formula for Area with Radius
The area of a circle is calculated by using π.
The formula for the area of a circle with the radius is as follows:
Area of a circle = πr2
Formula for Area with Diameter
Remember that radius is half of diameter.
So, for the area of a circle given diameter, use this formula:
Area of a circle = π × (D × 1/2)2
Values of π
π is equal to approximately 3.14.
However, you may see other more precise values for π, such as 3.142 or 3.14159.
Questions on Your Exams
Calculation with values
You may have to calculate the area of a circle based on the values provided.
Illustrations
You may also see questions asking you to study an illustration, and then calculate the area of a circle based on the illustration.
Differences of Areas
Exam questions also involve calculating the difference between the areas of two circles.
Practical Problems
There will also be practical questions about determining the area of circular objects.
Area of a Circle – Example Problems
Determine the answers to the following questions based on the facts provided.
Problem 1:
What is the area of a circle that has a radius of 8?
Problem 2:
What is the difference between the areas of the circles in the following diagrams?
Problem 3:
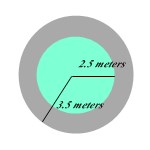
The city is going to build a pond in the local park.
The pond will have a walking path around it as shown in the grey part of the following diagram.
The walking path will be paved with a substance that costs $500 per square meter.
How much will it cost to pave the path? Use 3.14 for π.
Answers to the Area of a Circle Problems
Answer 1:
What is the area of a circle that has a radius of 8?
Use the formula provided above to solve the problem.
Area of a circle = πr2= π82 = 64π
Answer 2:
Here are the circles again.
First, calculate the area for each circle.
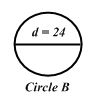
Area of circle A= πr2= π102 = 100π
Area of circle B = πr2= π122 = 144π
Note that the radius of circle B is 12 since radius is half of the diameter.
Then, subtract the area of the circle A from the area of circle B.
144π – 100π = 44π
Answer 3:
First, we need to find the difference between the area of pond and the area including the path and the pond.
Area of pond = πr2= 2.5 × 2.5 × 3.14 = 19.625 square meters
Area of a pond and path= πr2= 3.5 × 3.5 × 3.14 = 38.465 square meters
Then, subtract to find the area of path.
Area of path = 38.465 – 19.625 = 18.84 square meters
Finally, multiply by the cost per square meter in order to get the total cost.
Cost = 18.84 square meters × $500 per square meter = $9,420
Other Areas of Circles
What is a Sector?
A sector is a part of a circle that looks like a piece of pie.
To put it in geometric language, a sector is part of a circle enclosed between two radii.
The illustration below shows a sector:
Segments
A segment is a piece of a circle that is formed by a chord.
The top portion of the following circle is a segment:
A segment should not be confused with a semicircle.