Purpose of Trigonometric Functions
Trigonometric functions help us to understand relationships of the measurements of the sides of triangles to one another.
They can also help us to understand the relationships between measurements of other geometric shapes, such as chords and circles.
Trigonometric functions are essentially ratios containing the numbers or variables that represent these measurements.
If you are going to study engineering, trigonometric functions will help you to construct models.
You will also need to know trigonometric functions if you are taking an entrance exam that has a calculus component.
Trigonometric Functions – The Basic Concepts
Before we begin to talk about the six trigonometric functions, you should refer back to our post entitled “Sine Cosine Tangent.”
From that post, you will need to remember that the three sides of a triangle are the hypotenuse, the opposite side, and the adjacent side.
You will also remember from that post that three of the trig functions are sine, cosine, and tangent.
\(\text{sine} = \frac{opposite}{hypotenuse}\)
\(\text{cosine} = \frac{adjacent}{hypotenuse}\)
\(\text{tangent} = \frac{opposite}{adjacent}\)
Some students remember these trig functions by using the first letters of each of the equations:
SOH
CAH
TOA
Other students try to remember the basic functions as one word: SohCahToa
The Six Trigonometric Functions – Example
Having reviewed the basics, now let’s look at an example:
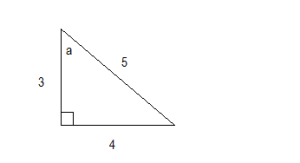
In our example triangle above, the side that measures 4 is the opposite side because it is across from angle a, which is the angle being measured.
The side that measures 3 is the adjacent side because it is next to angle a.
The side that measures 5 is the hypotenuse, because it is across from the right angle.
So, if we have a triangle with sides that measure 3, 4 and 5, we can form six different ratios.
Using the measurements of the sides with their descriptions, we get our six trigonometric functions:
\(\text{cosine} = \frac{3}{5} = \frac{adjacent}{hypotenuse}\)
\(\text{tangent} = \frac{4}{3} = \frac{opposite}{adjacent}\)
\(\text{sine} = \frac{4}{5} = \frac{opposite}{hypotenuse}\)
\(\text{secant} = \frac{5}{3} = \frac{hypotenuse}{adjacent}\)
\(\text{cosecant} = \frac{5}{4} = \frac{hypotenuse}{opposite}\)
\(\text{cotangent} = \frac{3}{4} = \frac{adjacent}{opposite}\)
The Reciprocal Trigonometric Functions
The secant, cosecant, and cotangent functions are called the reciprocal functions.
They are referred to as reciprocal because they flip the ratios of sine, cosine, and tangent.
“Flipping” the ratio means that they swap the position of the numerator and denominator in the particular ratio.
In other words, secant is cosine upside-down:
\(\text{secant} = \frac{hypotenuse}{adjacent}\)
Cosecant is sine upside-down:
\(\text{cosecant} = \frac{hypotenuse}{opposite}\)
Cotangent is tangent upside-down:
\(\text{cotangent} = \frac{adjacent}{opposite}\)
Further Problems on Trig Functions
As you can see, you can easily solve the reciprocal function if you have the values for its basic function.
Trigonometric identities are the relationships between the basic functions and the reciprocal functions.
Please see our post on Trigonometric Identities for further practice with trig functions.